NATURALEZA DE DIFICULTADES ASOCIADAS
AL APRENDIZAJE DE LAS MATEMÁTICAS: NÚMEROS ENTEROS, EN ESTUDIANTES DE GRADO OCTAVO DE EDUCACIÓN BÁSICA SECUNDARIA
Diego
Alejandro Cruz Echeverri
Universidad UMECIT, Panamá
profedace2009@hotmail.com
https://orcid.org/0000-0001-6888-5245
DOI: 10.37594/oratores.n17.695
fecha de recepción:21/09/2022 Fecha de revisión:15/10/2022 Fecha de aceptación:22/11/2022
RESUMEN
Este estudio considera el término “dificultades de aprendizaje” como unidad compleja de análisis ya que pueden ser diferentes factores los que inciden en su manifestación. Con el propósito de comprender su naturaleza, se retoman investigaciones relacionadas con el aprendizaje y algunas
de sus facultades de acuerdo con Claxton (2001) y Schunk (2012), el
conocimiento matemático, dificultades de aprendizaje en matemáticas y
evaluación. Como investigación cualitativa emplea la teoría fundamentada
(Strauss y Corbin, 2016) para la recolección de datos, el análisis y la
construcción de teoría a partir de los mismos y analizada con el apoyo del
software Atlas.ti; se desarrolla en el campo de la educación matemática para
realizar aportes en la comprensión de las dificultades que presentan los
estudiantes respecto al aprendizaje del número
entero.
Palabras clave: Aprender,
Dificultad de aprendizaje, Número entero, Teoría fundamentada.
NATURE OF DIFFICULTIES ASSOCIATED WITH LEARNING MATHEMATICS: WHOLE NUMBERS, IN EIGHTH
GRADE STUDENTS OF BASIC SECONDARY EDUCATION
ABSTRACT
This study considers the term “learning difficulties” as a complex
unit of analysis
since there may be different
factors that affect its manifestation. In order to understand its nature,
research related to learning and some of its faculties are taken up according
to Claxton (2001) and Schunk (2012), mathematical knowledge, learning difficulties in mathematics and
evaluation. As qualitative research, it uses grounded
theory (Strauss and Corbin, 2016) for data collection, analysis
and theory construction from
them and analyzed with the support of Atlas.ti software; It is developed in the
field of mathematics education to make contributions to the understanding of
the difficulties that students present with respect to learning the integer.
Keywords: learning,
learning difficulty, whole number, grounded theory.
INTRODUCCIÓN
Teniendo en cuenta que la presente investigación es desarrollada en el campo de la educación,
específicamente en lo concerniente al aprendizaje de las matemáticas y de
manera más puntual en relación a
dificultades asociadas al aprendizaje del número entero y, que la educación es asumida como un fenómeno social, se
propone su abordaje a partir de un enfoque investigativo que permita reconocer,
analizar y categorizar dificultades asociadas al aprendizaje del número entero que conduzcan a la comprensión de su naturaleza, con el propósito
de brindar elementos
que favorezcan su posterior tratamiento y abordaje desde los procesos de
enseñanza. A continuación, se esbozan los elementos que hacen parte de la
metodología de investigación, el posterior diseño de instrumentos, la
recolección de los datos y el análisis de los mismos a través de procesos de
codificación, mediados por el software Atlas.ti.
Enfoque de la investigación
Al partir de la necesidad de identificar la naturaleza
de dificultades asociadas al aprendizaje del número entero con
estudiantes de grado octavo de básica secundaria, que conlleve a una
categorización de ellas como propósito fundamental de este estudio, se considera
pertinente abordarlo desde un enfoque cualitativo, ya que centra su interés
en el identificar y reconocer
cuáles son las cualidades, características, acciones o comportamientos que
conducen a concluir la presencia de una dificultad de aprendizaje, ello a través de la observación, descripción e interacción, pues como lo señala Minayo (2010),
comprender e interpretar se convierten en los
principales verbos de la
investigación cualitativa. Se hace referencia a la complejidad, la sutileza y
la delicadeza del ver, oír, observar,
comprender e interpretar en la tarea del investigador, igual que en la vida diaria.
Del mismo modo, Minayo (2010) propone los sustantivos para
este enfoque, en relación a los dos verbos ya expuestos, “comprender e interpretar se fundamentan, epistemológicamente, en los siguientes sustantivos: experiencia,
vivencia, sentido común, acción social, significado e intencionalidad.” (p.254),
elementos a tenerse en cuenta en la tarea de reconocer la naturaleza de
dificultades asociadas al aprendizaje de las matemáticas, en relación al concepto matemático de los números
enteros, pues como ya se ha expuesto en el capítulo 1, se reconoce la presencia
de dichas dificultades, pero no se
vislumbra claramente su naturaleza, siendo un tema de interés tanto para
investigadores como para los mismos profesores de matemáticas.
De otra parte, Hernández, Fernández & Baptista
(2010) señalan que la complejidad y flexibilidad del enfoque cualitativo son mayores, en cuanto a la posibilidad de representarlo mediante un esquema circular, dado que
la secuencia puede variar y la indagación se mueve dinámicamente entre ambos sentidos: entre los hechos y su interpretación. De la misma manera, presentan las características, proceso y bondades para este enfoque:
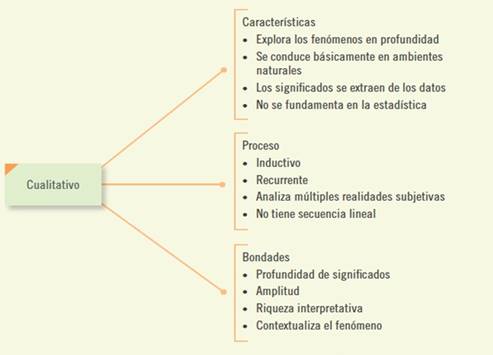
Imagen 1. Enfoque cualitativo Fuente:
tomado de Hernández, Fernández y Baptista (2010) p.3
Al respecto, es de resaltar,
entre sus características, el explorar los fenómenos en profundidad,
dado que hasta el momento
se han encontrado investigaciones referentes a dificultades en el
aprendizaje de las matemáticas más no se han ubicado
estudios en relación
a la naturaleza de éstas, situación que en el contexto en
que se ubica la investigación, amerita profundizar en un ambiente natural como lo es el aula de clase,
lo que conlleva a contextualizar el fenómeno y favorecer o posibilitar futuras investigaciones, de
tal manera que sea posible interactuar con los estudiantes, observar sus comportamientos al momento de realizar actividad
matemática poniendo a prueba
sus conocimientos, dialogar con ellos para así contrastar respuestas y pasar a
la identificación de posibles dificultades en el aprendizaje
de las matemáticas, en su abordaje a partir de
los números enteros, y un poco más allá, en el reconocimiento de su naturaleza, realizando así una inmersión en el objeto de estudio, tal como lo
amerita una investigación cualitativa, esto en el orden de contar con más de
una fuente que proporcione los datos necesarios para el desarrollo de la investigación.
Es importante mencionar que, desde la perspectiva de Hernández, Fernández y Baptista (2010), se asume que “la investigación cualitativa se enfoca a comprender y profundizar los
fenómenos, explorándolos desde la perspectiva de los participantes en un
ambiente natural y en relación con el contexto.” (p.364), de ahí la necesidad que este estudio
requiera de un método investigative que permita observar las
dificultades de aprendizaje desde la perspectiva de los estudiantes de la
institución educativa. Adicional a esto, aclaran que “es recomendable seleccionar el enfoque cualitativo cuando el tema del
estudio ha sido poco explorado, o no se ha hecho investigación al respecto en algún
grupo social específico.” (p.364), hecho del que se ha venido hablando
desde el capítulo 1 al no encontrar
investigaciones que hayan profundizado en la naturaleza de dificultades
asociadas al aprendizaje de las matemáticas, en tanto es común encontrar estudiantes en las aulas de clase
con indicios o manifestaciones de algún tipo de dificultad en su aprendizaje, y el conocimiento de su naturaleza podría
contribuir y favorecer la intervención para próximas investigaciones.
Se espera entonces, bajo este enfoque, realizar una
inmersión que permita recolectar los datos directamente en el ambiente, previa
definición de los lugares en los que se recolectarán y de los participantes que, para este caso, se
espera sea en el aula de clase y otros lugares propios y cercanos a la institución educativa, o en
su defecto, simulaciones de un ambiente escolar, con los estudiantes de grado
octavo y en relación con el concepto matemático números enteros. Así, se
posibilita observar los eventos que ocurren, simples o complejos, para
identificar aspectos explícitos e implícitos de los mismos,
sin puntos de vista o juicios de valor, mediante
la interacción con ellos y la
utilización de diversas fuentes. Esta observación tiene en cuenta a los participantes
en su contexto, y el investigador, además de registrar hechos, está en la tarea
de entender a los participantes (Williams, Unrau y Grinnell, 2005, citados en
Hernández, Fernández y Baptista, 2010), razón por la que se pretende, además de
respuestas escritas, buscar que los estudiantes puedan verbalizar y comunicar
los procesos y demás sucesos que esconden tras una respuesta, con el fin de
entenderlos y así construir camino hacia la comprensión de la naturaleza de
posibles dificultades en el aprendizaje de las matemáticas: números enteros, en
los casos que suceda.
Lo anterior remite a la necesidad de pensar en la
identificación de los datos a utilizar, de la misma manera que los
procedimientos a desarrollar y la forma de comunicar los resultados, dado que
no se han identificado estudios hasta el momento que logren resaltar un orden
de las dificultades en cuanto a su naturaleza, y de ahí el apremio por crear
teoría más que demostrarla, por tal motivo, el método que se considera más
pertinente es la teoría fundamentada, como un abordaje metodológico de tipo cualitativo, de acuerdo con Minayo (2010)
y Hernández, Fernández y Baptista (2010).
Teoría fundamentada
Strauss y Corbin (2016) definen
la teoría fundamentada como una “teoría derivada
de datos recopilados de manera
sistemática y analizados por medio de un proceso de investigación. En este
método, la recolección de datos, el análisis y la teoría que surgirá de ellos
guardan estrecha relación entre sí” (p.13). Su propósito es el de desarrollar teoría basada en datos
empíricos (Hernández, Fernández y Baptista, 2010) tal cual se planea la
recolección de datos a través de las respuestas obtenidas por parte de los
estudiantes, tanto escritas como orales, de manera sistemática, para proceder con su respectivo análisis y así llegar a la identificación de la naturaleza de dificultades asociadas al
aprendizaje de las matemáticas en relación al número entero. En ese sentido,
Strauss y Corbin (2016) plantean lo que definen como las características para
trabajar con la teoría fundamentada:
1.
Capacidad de mirar de manera retrospectiva y
analizar las situaciones críticamente.
2.
Capacidad de reconocer la tendencia a los sesgos.
3.
Capacidad de pensar de manera abstracta.
4.
Capacidad de ser flexibles y abiertos a la crítica constructiva.
5.
Sensibilidad a las palabras y acciones de los que
responden a las preguntas.
6.
Sentido de absorción y devoción al proceso del
trabajo. (p.8)
Se trata entonces de asumir dichas capacidades, no de
manera automática, pues se deben consolidar durante el proceso, en el sentido,
por ejemplo, de prestar especial atención a las respuestas que puedan dar los
estudiantes ante lo que puedan decir e incluso manifestar con su cuerpo,
situación que debe conducir a la retrospección y análisis crítico de los
hallazgos, evitando los sesgos y permitiendo la flexibilidad, elemento último
propio a la investigación cualitativa.
El planteamiento básico de su diseño, según Hernández,
Fernández y Baptista (2010), “es que las
proposiciones teóricas surgen de los datos obtenidos en la investigación, más
que de los estudios previos. Es el procedimiento el que genera el entendimiento
de un fenómeno” (p.493), siendo posible reconocer el valor que se le asigna
en la investigación, pues se trata principalmente
de trascender dificultades en el aprendizaje del número entero y comprender su
naturaleza, permitiendo que ella emerja a partir de los datos y su respectivo
análisis, al ir un poco más allá de las
respuestas que se puedan obtener como requisito para la categorización de las
mismas. De acuerdo con Strauss y Corbin (2016), dado que la teoría fundamentada
se basa en los datos, es más factible la generación de conocimientos, aumentar
la comprensión y proporcionar una guía significativa para la acción, ruta que
se pretende seguir para posibilitar la comprensión de dichas dificultades a
partir de su naturaleza, por medio de los procesos que evidencian los
estudiantes al enfrentarse a situaciones
que impliquen y requieran de la actividad matemática en relación al número
entero, como conocimiento matemático privilegiado en el estudio.
Teniendo en cuenta que “el
análisis es la interacción entre los investigadores y los datos” (Strauss y Corbin,
2016, p.14), parte
del proceso en la tarea
de identificar la naturaleza de dificultades
asociadas al aprendizaje de las matemáticas, en la interacción de los
estudiantes con situaciones relacionadas con el número entero, apunta al
reconocimiento de elementos internos y externos, tales como predisposiciones
por vivencias anteriores, dificultades propias con el conocimiento matemático,
ausencia de conocimientos previos como pre-requisitos o debilidad en ellos, la
relación profesor-estudiante que encarna asuntos emocionales, causas genéticas,
entre otras, esta investigación amerita de procesos rigurosos y sistemáticos,
dando cabida a la flexibilidad, para poder realizar un análisis coherente y
pertinente al problema estudiado. Uno de estos procesos es la codificación,
mencionado antes, cuyos propósitos son: construir teoría más que comprobarla;
ofrecer herramientas útiles para manejar grandes cantidades de datos brutos;
ayudar a considerar significados alternativos de los fenómenos; ser sistemático y creativo al mismo tiempo,
e identificar, desarrollar y
relacionar los conceptos, elementos constitutivos básicos de la teoría.
Procedimientos de codificación
Una vez identificados y recolectados los datos, viene el procedimiento de codificar, entendido como el “proceso
analítico por medio
del cual se fragmentan, conceptualizan e integran los datos
para formar una teoría” (Strauss y Corbin, 2016, p.3), importante para el
desarrollo de la teoría fundamentada, teniendo en cuenta que es un proceso de carácter dinámico
y que fluye como tal. Es
de anotar, en este punto, que “el análisis no es un proceso estructurado, estático o rígido”
(Strauss y Corbin, 2016,
p.64), haciendo referencia a la condición flexible propia de los métodos
cualitativos. Con esto, se encuentran tres elementos principales para el
análisis: los datos; las interpretaciones del investigador ante
acontecimientos, objetos, sucesos y acciones y,
en tercer lugar, la interacción
entre los dos elementos anteriores, en el proceso de recolección y análisis de
los datos.
En relación a los datos, esenciales en el proceso de
codificación, se espera su definición e identificación a partir de la propuesta
de Claxton (2001), específicamente lo que tiene que ver con las facultades para aprender, de tal
manera que se asumirán, en su ausencia, como posibles generadores de
dificultades en el aprendizaje de las matemáticas, a partir la propuesta y
ejecución de actividad matemática con los números enteros, y es allí cuando se
llega al conocimiento de su naturaleza, objetivo principal del presente
estudio. De acuerdo con lo anterior, será posible, según casos específicos, explicar algunas dificultades en razón a la resistencia que pueda existir
por parte del estudiante,
otras por la ausencia o mal uso de recursos internos y externos, o por la
calidad de la reflexión que se pueda generar en la relación estudiante –
conocimiento matemático.
Codificación
abierta
Este tipo de codificación, de acuerdo con Strauss y
Corbin (2016), se concibe como “el proceso
analítico por medio del cual se identifican los conceptos y se descubren en los
datos sus propiedades y dimensiones” (p.110), sentido en el que, en la
tarea de construir teoría, se convierte
en el primer acercamiento y tratamiento de los datos,
puesto que lleva directamente a la recolección de ellos, a partir de los
cuales emergen las categorías. De acuerdo con Hernández, Fernández y Baptista
(2010), el investigador debe revisar todos los segmentos del material para
analizarlos y así generar categorías iniciales de significado. En este caso, la
codificación abierta debe conducir a la generación de las primeras categorías
referidas a la naturaleza de dificultades asociadas al aprendizaje de las
matemáticas, específicamente del número entero, entendiendo por categorías
aquellos conceptos que representan fenómenos
(Strauss y Corbin,
2016), las cuales se basan en los datos
recolectados como lo son las observaciones, entrevistas, anotaciones, entre otros (Hernández,
Fernández y Baptista, 2010).
Como uno de los propósitos iniciales en la codificación es el
de determinar las propiedades y dimensiones de los datos, es importante tener
en cuenta que las primeras corresponden a las características de cada
categoría, mientras las segundas se refieren a la escala de variación de las
propiedades, tal como lo proponen
Strauss y Corbin
(2016). Ellos también
afirman, en el sentido de dar mayor claridad, que mientras “las propiedades son las características
generales o específicas o los atributos de una categoría, las dimensiones
representan la localización de una propiedad durante un continuo o rango” (p.128);
en este orden de ideas, la propuesta de Claxton (2001) en relación a las
facultades para aprender, se asumen como propiedades del objeto en estudio,
conduciendo así a la identificación de sus dimensiones a través del desarrollo
del mismo.
Se trata entonces
de identificar la naturaleza de posibles dificultades asociadas al aprendizaje de las matemáticas,
concretamente en lo referido al número entero, por tanto se parte de tres
facultades para aprender: resistencia, recursos y reflexión, definidas por
Claxton (2001), y las cuales se tornan en posibles dificultades en la medida
que es considerada su ausencia y, en
base a ellas, realizar el proceso de codificación abierta según lo expuesto.
Una vez se logren identificar y
definir las categorías, de acuerdo a sus propiedades y dimensiones, se procede
con la codificación axial, tratada a continuación.
Codificación axial
Definida por Strauss y Corbin (2016) como el “proceso de relacionar las categorías a sus subcategorías, denominado -axial-
porque la codificación ocurre alrededor del eje de una categoría, y enlaza las
categorías en cuanto a sus propiedades y dimensiones” (p.134), su propósito es precisamente el de iniciar
el proceso de reagrupar los datos, relacionando categorías y
subcategorías para lograr explicaciones más precisas sobre el objeto de estudio.
Nuevamente se retoman las propiedades y dimensiones para
establecer dichas relaciones, como ya se ha mencionado, teniendo en cuenta que “una categoría representa un fenómeno, o
sea, un problema, un asunto, un acontecimiento o un suceso que se define como
significativo para los
entrevistados” (Strauss y Corbin, 2016, p.136), buscando la identificación
y reconocimiento de la naturaleza de dificultades asociadas al aprendizaje en
el área de las matemáticas, a partir de actividad matemática en el campo de los
números enteros.
De acuerdo con Hernández, Fernández y Baptista (2010), en
este tipo de codificación se parte del análisis en la agrupación de los datos,
previamente separados durante la codificación abierta, proceso en el que “se construye un modelo del fenómeno
estudiado, que incluye: las condiciones en que ocurre o no ocurre, el contexto
en que sucede, las acciones que lo describen
y sus concecuencias” (p.494), que en el caso propio, y como ya se ha
expuesto antes, refiere a la identificación de la naturaleza de dificultades
asociadas al aprendizaje de los números enteros, para la posterior
categorización de las mismas, siendo, por consiguiente, un proceso más
analítico comparado con la codificación abierta, en la que se requiere de mayor abstracción.
Como uno de los propósitos de la codificación axial es el establecimiento de relaciones entre categorías a partir de los datos,
Hernández, Fernández y Baptista (2010) las conciben
como “temas de información básica
identificados en los datos para entender el proceso o fenómeno al que hacen referencia” (p.495), dichas categorías deben conducir entonces a comprender dificultades asociadas al aprendizaje de las matemáticas a partir de la
identificación de su naturaleza. Señalan, además, la utilidad de la teoría
fundamentada, concretamente en la comprensión de procesos educativos, al identificar conceptos implicados y la
serie de acciones e interacciones de quienes se involucran en el proceso.
Codificación selectiva
Para Hernández, Fernández
y Baptista (2010),
el principal atributo
de la teoría fundamentada
consiste en que “los datos se categorizan
con codificación abierta, luego el investigador organiza las categorías resultantes en un modelo
de interrelaciones (codificación axial), que representa a la teoría emergente
y explica el proceso o fenómeno de estudio” (p.496), para posteriormente
llegar a la integración y refinamiento de la teoría (codificación selectiva),
tal como lo definen Strauss y Corbin (2016).
De acuerdo con lo anterior, en primera medida
se procura identificar y generar las categorías
y propiedades que representan la naturaleza de dificultades asociadas
al aprendizaje de los números enteros, para posteriormente
establecer relaciones entre dichas categorías y las subcategorías que puedan
emerger a partir de ellas y, luego, dar paso al refinamiento e integración de
la teoría, como fin de la teoría fundamentada.
Para llegar a la integración de la teoría,
proceso que requiere
de tiempo y no sucede
de la noche a la mañana, tal como lo afirman Strauss y Corbin (2016),
se requiere de la interacción entre los datos
y el analista, que incluye
“la evolución del pensamiento que ocurre con el tiempo
gracias a la inmersión en los datos” (p.158), haciendo
referencia al investigador y su arduo trabajo. Es posible
que al inicio no sea tan fácil identificar y reconocer los datos, sus
categorías y subcategorías, pero se sugiere entonces que la inmersión en ellos
y las relaciones que se puedan establecer, favorece los procesos de
codificación en sus diferentes niveles, para así llegar a la integración de la
teoría. Se hace referencia igualmente a que el investigador, o analista, “reduce datos de muchos casos a conceptos y los convierte en conjuntos de
afirmaciones de relación que pueden usarse para explicar, en un sentido general, lo que ocurre” (p.159), de
tal forma que, para el presente estudio, se requiere tener claridad frente a lo
que pueda ser o no una dificultad en el aprendizaje de las matemáticas, y para ello será necesario
contrastar los datos a través de varias fuentes, y no limitarse a una sola, y a partir de ellas
generar esos conceptos o relaciones que lleven al establecimiento de categorías
y permitan continuar con el proceso.
Para determinar los datos, se piensa en enfrentar a los
estudiantes, foco de la investigación, al desarrollo de una guía física, en relación al conocimiento matemático previamente seleccionado
e identificado, números enteros, para posteriormente contrastar las respuestas
que se obtengan por parte de ellos en
una entrevista semiestructurada, a fin de que se les permita verbalizar lo que
puedan sentir, saber o pensar en la solución
de la primera guía, con la intensión de permitirse ir más
allá de las respuestas y comprender qué condiciones, características o procesos
se esconden tras ellas, en un análisis más profundo de las mismas.
Para lograr tal integración de los datos en teoría, el
primer paso consiste en la determinación
de la categoría central (Strauss y Corbin, 2016), la cual se convierte en la
representación del tema principal de la investigación, que para el presente estudio
corresponde a la naturaleza de dificultades
asociadas en el aprendizaje de las matemáticas, concretamente de los números
enteros. Entre las técnicas para facilitar tanto la identificación de la
categoría central como la integración de los datos, Strauss y Corbin (2016)
sugieren algunas, como el relatar la historia, el uso de diagramas y la revisión
y clasificación de memorandos a mano o a través de software
especializados, como sería el caso de Atlas.ti.
Análisis a partir de la teoría
fundamentada
La selección de la teoría fundamentada obedece al
propósito de explicar un fenómeno determinado
a partir de la creación
de teoría, pasando
por procesos de codificación que conllevan a la generación de categorías, las cuales en su integración y establecimiento de relaciones conducen
a que emerja la teoría, punto
en el que el uso de esquemas
se identifica como necesario y pertinente,
lo anterior teniendo en cuenta que hasta el momento no se han encontrado
investigaciones que profundicen en su estudio y comprensión, y más que
demostrar teoría, se busca la creación de la misma.
El presente estudio se centra en el análisis de
procesos, características, comportamientos, condiciones, que se esconden en
estudiantes de grado octavo con posibles dificultades en el aprendizaje de las matemáticas, concretamente con los números enteros,
situación que corresponde al fenómeno de estudio, objeto
de la investigación.
Trabajo de campo
En una investigación de corte cualitativo, y partiendo de las metas
trazadas, se requiere
de la interacción con la población
objeto de estudio,
que para el presente caso corresponde a estudiantes
que cursan el grado octavo de educación básica secundaria. Por lo tanto, el
trabajo de campo está centrado en la planeación y ejecución
de actividades que posibiliten el reconocimiento y análisis de la naturaleza de dificultades asociadas
al aprendizaje, cuando ellos se enfrentan al desarrollo
de actividad matemática referida a los números enteros. Dadas las características del método de investigación seleccionado, se identifican y detallan algunos
elementos que encaminan este estudio.
Se espera de la interacción en ambientes reales de clase
en la institución educativa que hace parte del presente estudio, o en su
defecto, realizar una simulación de las mismas, poder participar en clases de matemáticas con estudiantes que cursan
el grado octavo, en las que la actividad matemática se centre en la verificación de aprendizaje de los números
enteros. En primera
instancia, se pretende identificar qué estudiantes evidencian posibles
dificultades en el aprendizaje de los mismos,
contrastando respuestas escritas
con las que puedan verbalizar, con el detalle
y rigurosidad que se amerita,
pues a partir de allí se obtendrán los datos y se iniciará el proceso de
codificación correspondiente, tal cual se ha descrito en este capítulo.
Una vez se observen e identifiquen estos estudiantes, se
procede con la tarea de reconocer elementos que se esconden tras las evidencias
de posibles dificultades, en tanto se permita señalar regularidades,
similitudes y diferencias entre ellos, proceso correspondiente a la
codificación abierta, para posteriormente establecer y definir
las relaciones entre
los elementos seleccionados que posibiliten la delimitación de categorías, las cuales
agrupan y representan el fenómeno en estudio, tarea de la codificación axial,
esto en el ejercicio de reconocer las propiedades y características que conlleven
a la identificación de relaciones entre las mismas.
En este punto, es importante tener en cuenta las respuestas que ofrecen los estudiantes, no
sólo escritas sino verbales también, en la medida que se les da la posibilidad
de verbalizar los procesos que siguieron para llegar a ellas, además de sus
actitudes, gestos o silencios.
Técnicas para la recolección de
la información
Partiendo de los elementos anteriormente señalados, se contempla
el uso de dos instrumentos principales que posibiliten
la recolección de los datos. El primero de ellos, corresponde al diseño de una
guía – taller, la cual propone a los estudiantes una serie de ejercicios que
promueven el desarrollo de actividad matemática, desde el conocimiento de los
números enteros, tal como se ha
descrito en los Estándares Básicos de Competencia en Matemáticas (MEN, 2006). Teniendo en
cuenta las respuestas obtenidas por ellos, se procede con la identificación de
aquellos que muestran dificultades, al basarse en las mismas respuestas, es
decir, quienes no hayan respondido correctamente, proceso que se seguirá a
través de las evidencias de aprendizaje descritas en la matriz diseñada
para tal fin. Con estos
estudiantes, se lleva
a cabo una entrevista semiestructurada, buscando que puedan
exponer, de manera verbal, lo sucedido durante su interacción con la guía.
Atlas.ti
Atlas.ti es una herramienta de uso tecnológico y técnico
creada con el objetivo de apoyar la organización, el análisis e interpretación
de información en investigaciones
cualitativas, permitiendo el trabajo y organización de grandes cantidades de
información en una variedad de formatos digitales, además de favorecer la
comparación, optimizando de esa forma los tiempos en la investigación y mejorar
el aprovechamiento de la información en el tratamiento de los datos.
Este software posibilita la segmentación de datos en
unidades de significado, la codificación
de los datos y la construcción de teoría (relacionar conceptos y categorías),
tal como lo plantean Hernández, Fernández & Baptista (2010), y que para la
teoría fundamentada corresponden a los tres
procesos de codificación (abierta, axial y selectiva). Atlas.ti
dispone diversas herramientas para efectuar tareas asociadas
con enfoques sistemáticos para datos no estructurados, es decir, datos que
no se pueden analizar de manera significativa mediante enfoques estadísticos formales, ayuda en la
exploración de los complejos fenómenos ocultos en sus datos, para lo cual ofrece herramientas para gestionar, extraer, comparar, explorar y volver a montar
piezas significativas a partir de grandes cantidades de datos de forma
creativa, flexible pero sistemática.
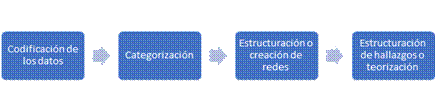
Varguillas (2006) comparte, en primera instancia, la siguiente recomendación
metodológica para quien realiza investigación cualitativa:“uso del programa computacional Atlas.ti como herramienta de apoyo al
proceso de anális” (pág.75), dado que puede trabajar con diversas fuentes
de información, desde textos, observaciones, audios, entre otros. De esa
manera, describe el programa en la medida que el proceso implica cuatro etapas,
las cuales ya fueron descritas en el
apartado de teoría fundamentada y los procesos de codificación, a saber:
Imagen 2. Etapas
Atlas.ti. Elaboración propia. (Varguillas, 2006, pág. 76)
San Martin (2014) considera este software como el
principal soporte informático para desarrollar teoría fundamentada, entre otras
razones, porque favorece la identificación de los códigos que requieran saturación, a través de sus funciones tanto para cada código como categoría,
orientado hacia la conceptualización, en el que “cada paso de la codificación teórica (codificación
abierta, axial y selctiva) tiene un espacio en el programa” (pág.114). La
primera de ellas, codificación abierta, se da con la asignación de códigos a
citas, en los formatos posibles, mientras que
la codificación axial surge con la creación
de redes de relaciones conceptuales y, para la tercera, Atlas.ti dispone de funciones que
permiten establecer una categoría central, momento en el que se integran los
códigos y categorías establecidos para tal fin.
Por lo anteriormente expuesto, dados los aportes de los
diferentes autores citados y por las características de este estudio, teniendo
en cuenta que la teoría fundamentada emplea diversos procesos de codificación,
se considera y asume el uso del Atlas.ti como un apoyo relevante en la tarea de
establecer relaciones entre los datos y llegar a categorizar dificultades
asociadas al aprendizaje del número entero según sea su naturaleza.
Análisis
Para esta investigación el análisis ocupa
un lugar predominante, en tanto que
se busca encontrar y determinar conexiones entre
posibles dificultades asociadas al aprendizaje del número entero, especialmente
a sus orígenes o causas, asumidas en este caso como su naturaleza,
convirtiéndose así en un proceso continuo que abarca desde principio a fin y
que busca dar cumplimiento a los objetivos trazados, responder
a la pregunta formulada y al mismo tiempo dar validez a los resultados obtenidos.
Identificar posibles dificultades relacionadas con el
aprendizaje del número entero en estudiantes de octavo grado, en un ambiente
cotidiano para ellos, se convierte en el primer paso para llegar a establecer
relaciones entre ellas y sus potenciales causas. Para este caso, es de anotar
que si bien el proceso de aprendizaje puede diferir de una persona a otra, por
lo que no se podría generalizar o disponer
reglas, lo que se busca es identificar y establecer regularidades que faciliten su reconocimiento dentro del aula,
situación que pretende
brindar una mayor
posibilidad de atención por parte del docente,
contemplando la factibilidad de retomar los resultados obtenidos para el
desarrollo de futuras investigaciones. Durante el proceso de descripción y análisis
se presentarán algunas imágenes tomadas de las respuestas proporcionadas por
los participantes, a fin de mostrar el proceso de análisis realizado a partir
de los datos.
Recolección de los datos
La recopilación de los datos para el desarrollo del presente
estudio, tal como se planteó anteriormente,
se dio en la institución educativa de la cual forman
parte los estudiantes, un ambiente natural y
cotidiano para ellos tal como lo proponen Hernández, Fernández & Baptista
(2010). Inicialmente, previo diálogo y concertación con los participantes, se
procede con la aplicación del primer instrumento (guía taller), a partir del cual
se obtienen algunas evidencias de aprendizaje respecto al conocimiento
matemático del número entero, de acuerdo a lo planteado en la matriz diseñada
para tal fin pero, así mismo, ante la no presencia de dichas evidencias se
identifican posibles dificultades asociadas al aprendizaje de él, de esta
manera se selecciona una muestra en virtud de las características de las
respuestas y, partiendo del propósito
de esta investigación, se procede con el proceso de codificicación y análisis.
Para esta investigación, los datos corresponden inicialmente a las respuestas que dan indicios de posibles dificultades y que fueron obtenidas luego de la aplicación del primer instrumento a partir del
desarrollo de actividad matemática en torno al número entero. Posterior a ello,
las respuestas a las preguntas
planteadas en la entrevista semiestructurada se suman al cuerpo de los datos,
los cuales serán tratados a través de Atlas.ti en los diferentes procesos de codificación.
Respuestas escritas
proporcionadas por los participantes
Partiendo de las respuestas de la guía taller
suministradas por los estudiantes, se observan indicios conducentes a la
posible presencia de dificultades asociadas al aprendizaje del número entero,
como se muestra a continuación:
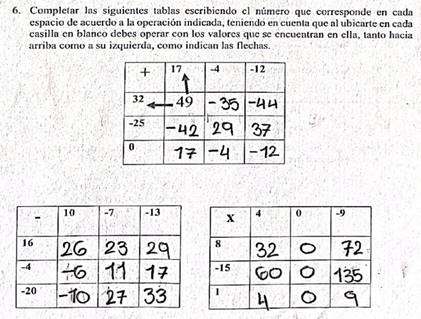
Imagen 3.
Respuestas instrumento 1
Para este caso, como se indica en el enunciado, la actividad matemática consistía en completar cada uno de los espacios
teniendo en cuenta la operación presente (suma, resta o multiplicación) pero,
además, atendiendo al concepto de número entero y las implicaciones de los
signos (más, menos). Dado que los EBC en matemáticas abordados corresponden al
ciclo de los grados 6º y 7º, se esperaría que estuviesen en la capacidad de
responder acertadamente mostrando así evidencias de aprendizaje, sin embargo,
es posible observar
por ejemplo en el primer recuadro correspondiente a la operación suma, que:
32+(-12)=-44
-25+17=-42
-25+(-4)=29
-25+(-12)=37
Las respuestas anteriores son incorrectas pues se
observa que, sin importar los signos, en todos los casos realiza operaciones de
suma, así como también se puede intuir que desconoce el significado del símbolo
menos y las propiedades multiplicativas de los signos. Sin embargo, dadas las
condiciones y características de este estudio, será necesario ir un poco más
allá de ellas a través del diálogo que se pueda generar por medio de la
entrevista semiestructurada, buscando así la identificación del por qué de
dichas respuestas, entendida esta como su naturaleza dentro de la investigación en desarrollo. Ahora
bien, haciendo referencia nuevamente a las respuestas y al retomar la matriz elaborada para su análisis,
es posible señalar dificultades en las siguientes evidencias de aprendizaje,
siendo viable determinarlo al reconocer su ausencia:
•
Resuelve problemas en los que intervienen cantidades
positivas y negativas
•
Propone y justifica diferentes estrategias para resolver problemas con números enteros
•
Interpreta y justifica cálculos numéricos al
solucionar problemas.
•
Propone y utiliza diferentes procedimientos para
realizar operaciones con números enteros
•
Describe
situaciones en las
que los números
enteros y sus
operaciones están presentes.
•
Utiliza los signos “positivo” y “negativo” para
describir cantidades relativas con números enteros
•
Describe procedimientos para calcular el valor de una operación (suma, resta, multiplicación y división) entre números enteros.
De manera similar sucede con la resta y multiplicación
entre números enteros, dado que al igual que en la suma, se observa que las
respuestas no coinciden con la operación indicada, situación que abre el camino
para pensar en posibles dificultades relacionadas al aprendizaje del número entero.
En el caso de la división entre
números enteros, nuevamente se observan dificultades frente al tratamiento de los
signos, aún cuando con el instrumento se les proporcionó información referente
a las cuatro operaciones básicas, abordadas en la guía taller y que se esperaba
pudiesen utilizar para facilitar el desarrollo de la misma.
Ir más allá de respuestas
escritas
Una vez implementado el instrumento 1 y luego de revisar
y seleccionar aquellas respuestas que dan indicios de dificultades asociadas al
aprendizaje del número entero, se procede de igual manera con la invitación a
cada uno de los participantes elegidos para llevar a cabo el proceso de
diálogo, orientado por la propuesta
de entrevista semiestructurada y contando además
con la debida autorización de sus padres ya que, siendo menores de
edad, es necesario dicho permiso para poder
realizar las grabaciones y así mismo para el tratamiento de su información. De
esta manera, el espacio seleccionado para tal fin sigue siendo el colegio, como
ambiente natural y cotidiano para ellos, según lo planteado por Hernández,
Fernández & Baptista (2010).
Dado su propósito, se lleva a cabo el encuentro con cada uno de los participantes previamente seleccionados, procurando no
intimidarlos ni generar inconvenientes en ellos con la dinámica propuesta, sino
más bien tratar de hacerlo de la mejor forma posible en un ambiente en el que se
sientan cómodos y que puedan expresar sin temor lo que deseen, en concordancia
a las preguntas planteadas y las que vayan surgiendo en medio de la conversación. En este sentido,
se hace claridad respecto a que no habrá respuestas correctas
o incorrectas, el ejercicio consiste precisamente en tener
la posibilidad de, a partir de sus respuestas iniciales
en el instrumento anterior, ir un poco más allá para conocer el por qué de
ellas, que lo puedan exponer y verbalizar con
total confianza. En este proceso
es posible apreciar
que, en general,
se asocia el número entero
con pérdidas y ganancias, pero no se evidencia claridad
frente a la apropiación del concepto matemático abordado.
Se consideran por medio de las respuestas
manifestaciones de dudas en lo que verbalizan y así mismo con los silencios que se hacen presentes por momentos, hechos
que se interpretan como
expresiones de dificultades en la comprensión y claridad frente
al concepto de número entero,
y que como tal ejerce influencia en la realización de actividad matemática que le involucra. Inicialmente, los participantes asumen que les va bien en
matemáticas, esto según lo expresan ellos mismos; durante el diálogo previsto,
reconocen la presencia tanto de agentes externos como internos en sus procesos de aprendizaje para el caso
concreto frente al número entero, entre ellos la falta de atención y el papel
que desempeña el maestro.
Los diálogos permitieron identificar la importancia de
lo planteado por Claxton (2001) en relación a los recursos internos y externos,
como parte importante de la facultad de aprender, situación que se puede corroborar en las respuestas ofrecidas por ellos.
Es así como podría pensarse en cuáles recursos afectan el
proceso de aprendizaje del número entero, que para este caso se identifican
aspectos como el tiempo, la atención, la relación con docentes, la disposición
para el trabajo, entre otras, elementos que son tomados
para definir las propiedades y dimensiones que las
pueden constituir en categorías. De esta manera y con la ayuda de Atlas.ti se
aborda el proceso de codificación abierta, centrando la atención en las
diferentes manifestaciones de las dificultades en las explicaciones dadas por
los participantes.
En este orden de ideas y en la tarea de identificar qué se esconde
tras las posibles
dificultades en el aprendizaje del número entero vistas en los
argumentos recibidos, se reconoce además la dificultad que genera el uso de los
números enteros en el desarrollo de operaciones básicas entre los
participantes, con lo que se hace alusión a la naturaleza de los mismos y
reafirman también los hallazgos
registrados en las respuestas escritas, extraídas del primer instrumento.
Destaca durante el proceso de análisis, como se ha mencionado, el conflicto que les genera el uso de los signos más y menos en el desarrollo de dichas operaciones, mencionado de manera explícita por ellos cuando, por ejemplo, en lugar
de sumar restan
o, al contrario, aludiendo que en algunos
casos puede deberse al no tener en cuenta dichos
signos y que, como se indica, se demuestra en las respuestas señaladas y el análisis realizado en el apartado anterior.
En relación a las clases de matemáticas, en general
manifiestan agrado hacia ellas, en lo que
incluyen tanto las metodologías como a los profesores que han ocupado ese
lugar, sin embargo, son conscientes y
reconocen también los inconvenientes
que genera la falta de atención frente a las explicaciones y el desarrollo de las
actividades asignadas. Ya sobre el
caso concreto del número entero, al comparar un entero negativo con el cero
coinciden en que este último es menor aduciendo a previas explicaciones del
profesor, según lo pueden manifestar; en algunos casos hay claridad frente
a lo que se debe hacer, pero no logran
hacerlo, evidenciando así confusión al realizar
actividad matemática que involucra números enteros.
Análisis de los datos, procesos
de codificación
Entendidos los datos como las respuestas que evidencian
dificultades en el aprendizaje del número
entero se procede
con el ingreso de las entrevistas, fuente de los mismos, al software Atlas. ti, al inicio como archivos de
audio y luego la transcripción de las mismas, dado que en formato de texto
se facilita la asignación de códigos a las citas seleccionadas, para así dar
inicio al proceso de codificación con la fragmentación de los mismos de
acuerdo a sus propiedades y dimensiones.
Causas asociadas
a dificultades en el aprendizaje
del número entero, descubrir propiedades en los datos
Como primer proceso
de codificación, en concordancia con la teoría
fundamentada (Strauss & Corbin, 2016), se inicia
con la tarea de identificar similitudes a los datos en tratamiento, de manera
tal que, sea posible asignar
códigos a las citas que se vayan
seleccionando. De esta manera, algunas de esas propiedades se reconocen
a partir de los soportes teóricos mientras otras van surgiendo de los mismos
datos, es decir, de las respuestas dadas. A continuación, se presenta una
síntesis del trabajo realizado con la mediación de Atlas.ti; la siguiente
imagen muestra en la columna central los datos (respuestas de los
participantes) mientras que a su derecha se identifican las propiedades
(códigos) asignadas a cada cita:
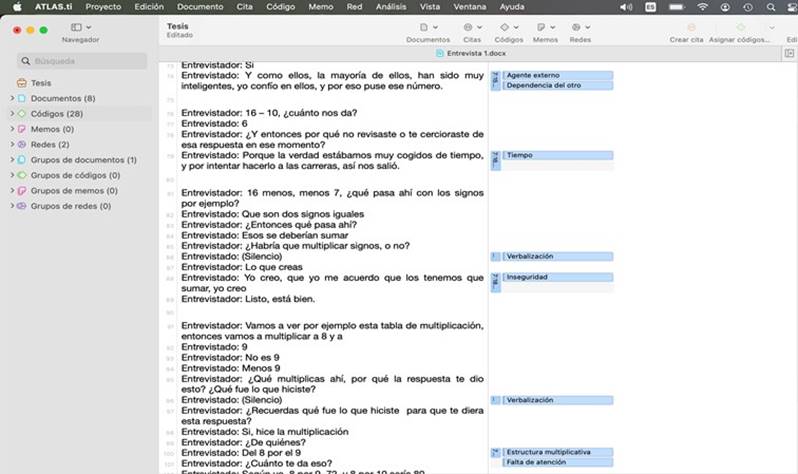
Imagen 4. Ambiente Atlas.ti, procesos de codificación.
Esta revisión se realiza con cada una de las fuentes (entrevistas) mientras el software
recopila los códigos que se van asignando. Es posible identificar que la
falta de atención y así mismo la comprensión surgen en los datos al tratar de
explicar el por qué de las respuestas dadas, esto en la medida que se reconoce
a la falta de atención como una de las posibles causas asociadas al aprendizaje
del número entero que, a su vez, genera incomprensión. En este orden de ideas,
también aparece el factor tiempo al desempeñar un papel poco favorable cuando
de realizar actividad matemática se trata, y así otros códigos más que se
detallarán en lo que sigue y que se pueden ir relacionando con los recursos
necesarios para el aprendizaje (Claxton, 2001).
En un primer
ejercicio de identificar regularidades entre los datos, durante la codificación
abierta, se obtienen los siguientes códigos:

Imagen 5. Nube de códigos,
codificación abierta.
Através del softwareAtlas.ti, en apoyo a estos procesos
de codificación, se consolida la anterior
nube de códigos en la que se vislumbran propiedades relacionadas con ellas y en correspondencia a condiciones necesarias para el aprendizaje. En este sentido,
resalta la comprensión entre las demás por encontrarse ubicada en el centro
y también por su tamaño,
lo que significa que es el código
que se asignó mayor cantidad de veces durante el proceso y que se puede
constatar por medio de un diagrama de barras, proporcionado por el mismo programa:
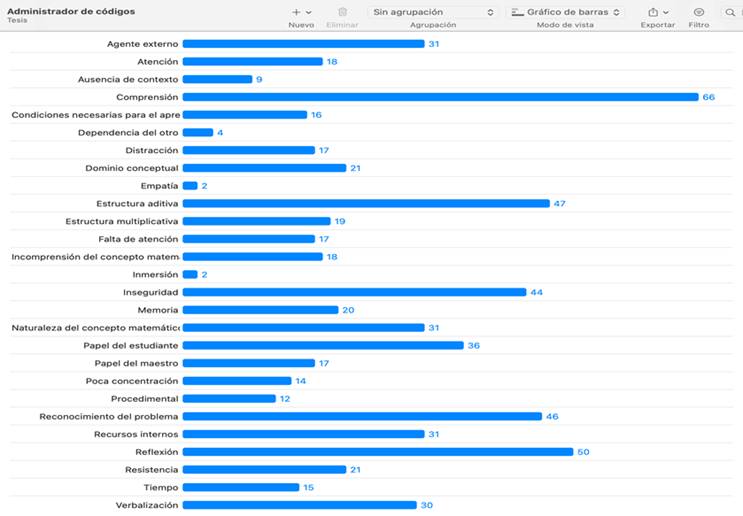
Imagen 6. Diagrama de
barras porporcionado por Atlas.ti
Es posible apreciar, partiendo del diagrama anterior,
que el término comprensión encabeza la lista, seguido de reflexión, estructura
aditiva, reconocimiento del problema, inseguridad, papel del estudiante y
agente externo, naturaleza del concepto matemático y recursos internos con una
frecuencia igual, entre los que siguen. Como lo señala la codificación abierta,
estos términos se definen teniendo en cuenta códigos
creados a partir de las propiedades y regularidades de los datos; en este estudio se asignaron
basados en las características asociadas al fenómeno, a continuación, se
explica la manera como se asignaron algunas de
ellas.
La comprensión se define inicialmente como una categoría
ya que se identifica de manera regular en los datos de diferentes formas, por
ejemplo: al tratar de explicar el por qué se
presentan dificultades en el aprendizaje del número entero; al
identificar la falta de comprensión de lo que se debe hacer (enunciados,
instrucciones, indicaciones, …) como la comprensión del concepto matemático en
sí, referidas de otra forma como conocimiento procedimental y conocimiento
conceptual. De otro lado, se identifican variaciones en esta categoría lo cual
conlleva a prestar atención a niveles en la comprensión, puesto que puede
tenerse claridad frente a lo que hay que hacer o cómo hacerlo, pero no disponer
del dominio conceptual para lograrlo o viceversa, esto se interpreta dentro de la teoría
fundamentada como dimensiones. Esta categoría surge, como se indica, al
identificar que asocian al número entero con pérdidas y ganancias, sin
posibilidad de evidenciar mayor apropiación del concepto matemático, asdemás de manifestar de dudas en lo que dicen y presencia de silencios por momentos.
Es así como se reconoce una subcategoría asociada a la
comprensión, correspondiente a la capacidad
para verbalizar, ya que es una forma de dar a entender
a otro qué tanto se ha comprendido o, por el contrario, dar
muestra de que no se comprendió lo requerido, y que se relaciona también con el
nivel de seguridad o inseguridad que se demuestra, asumiéndose como otra
subcategoría en relación, aspectos
que serán verificados en las siguientes codificaciones.
De forma similar,
surge en los datos otra categoría referente
al uso del tiempo, el cual se puede
evidenciar en diferentes momentos y respuestas expresadas por los participantes, se reconoce como una regularidad que puede afectar el
aprendizaje del número entero. Además de lo anterior, son argumentos
presentados para justificar sus resultados en el desarrollo del primer instrumento.
De esta manera, el manejo del tiempo es una categoría
inicial que se identifica durante este proceso de codificación y como tal,
presenta dimensiones relacionadas con su duración, es decir, con su frecuencia
y puede ser en menor o mayor cantidad su aprovechamiento, tanto al momento de
realizar actividad matemática como de atender a las explicaciones, razón por la
que es posible relacionarla con otras subcategorías como lo son la falta de
atención, los recursos internos o poca concentración, extraídas igualmente de
los datos en el proceso de codificación y análisis dentro de la codificación axial. En este sentido, el reconocimiento de notoria distracción, poca concentración
ante explicaciones o desarrollo de actividades asignadas se relacionan como
subcategorías para el manejo del tiempo.
Otra regularidad identificada en los datos es la que se
define como reconocimiento del problema, en tanto que se identifican respuestas
que evidencian directamente que los participantes
reconocen problemas para abordar el tema de números enteros,
lo cual puede ser consciente de que se está haciendo algo mal, así como también
de que se están cometiendo errores o asumir lo que se plantea
como difícil, incluso
reconocer que el desarrollo de actividad matemática que involucra al número
entero implica dificultad y en algunos
casos el concepto
matemático en sí mismo, estos aspectos pueden
ser variaciones que conllevan a señalarse como dimensiones en tanto que se identifican la necesidad
de solucionar dicho problema, puesto que puede
variar entre individuos, algunos
estarán interesados en hacerlo mientras
que otros no, o al menos no con la intensidad y disposición o motivación
requerida, también se señala la actitud que se
pueda asumir posterior a dicho reconocimiento, lo que conlleva
a actuar en diversas circunstancias que dependen de ello,
aspectos que se retomarán en la codificación axial para refinar
el alcance de esta categoría.
Otra característica común se reconoce al hacer
referencia al concepto de número entero, partiendo de la presencia de los
signos más y menos y la interpretación que se le da a los mismos,
convirtiéndose en una regularidad dentro de los datos. Es así como se denomina
la categoría uso de signos, que implica propiamente las propiedades de dos estructuras: aditiva y multiplicativa, las cuales llegan a generar confusiones en el desarrollo de
operaciones que les implican, es ahí, por ejemplo, cuando se multiplican signos
en casos que no aplica, se suma cuando había que restar o viceversa, en correspondencia con sus dimensiones. Se considera esta categoría como significativa
ya que se observó en diferentes momentos
durante el desarrollo de la guía y en varios participantes. Se nombra uso de signos,
dado que se identifica conflicto que genera el uso de los signos más y menos en
el desarrollo de operaciones básicas (suma, resta, multiplicación, división),
como se demuestra con algunas respuestas de los participantes.
En conjunto, durante
este proceso de codificación abierta,
se pueden identificar las siguientes
categorías en relación a naturaleza de dificultades asociadas al aprendizaje
del número entero con estudiantes de octavo grado: comprensión, manejo del
tiempo, reconocimiento del problema y uso
de signos, nombres que son asignados teniendo en cuenta las propiedades y
dimensiones de los conceptos estudiados.
Lo anterior, se convierte en un primer
acercamiento al proceso
de codificación y determinación
de causas asociadas al objeto de estudio definido, las cuales se espera
precisar y definir por medio de los siguientes procesos de codificación.
CONCLUSIONES
Apartir del tratamiento de datos planteado por la teoría
fundamentada (Strauss y Corbin, 2016), se han diseñado instrumentos que
permitan la interacción de los participantes en situaciones que implican los
conocimientos y procesos asociados al número entero, con el propósito de
identificar y analizar la naturaleza de posibles dificultades de aprendizaje
asociadas a dicho conocimiento.
Es importante anotar que fue necesaria la implementación
de entrevistas semiestructuradas para ampliar la mirada de otros datos que
permitieran identificar posibles
dificultades en torno al aprendizaje
del mismo, posiblemente desde lo cognitivo y los recursos para el aprendizaje
enunciados por Claxton (2001), partiendo de las respuestas iniciales aportadas por los participantes las cuales se retoman como
datos para su análisis y tratamiento. La codificación de los datos permitió el
reconocimiento de diferentes categorías, por
ejemplo:
Uso de signos (estructura aditiva y multiplicativa): se identifica
conflicto que genera el uso de los signos más y menos en el desarrollo de
operaciones básicas (suma, resta, multiplicación, división) cuando, por
ejemplo, en lugar de sumar se resta o al contrario; presente en casos como: “Por lo malo,
me ha ido un poquito
así con los números enteros,
que al sumarlos, que al restarlos y que saber cual es el menor y cual es el mayor, esa es la dificultad que tengo”; “Es que yo me troco mucho con eso, todos
nos trocamos con los signos”;
“Porque se nos olvida y nos trocamos. A veces hay tantos,
tantos signos que uno dice, entonces este de cuál es y este de cuál es, si me
entiendes, entonces hay dificultades en eso.”
Incomprensión del concepto: Asociación del número entero con
pérdidas y ganancias, sin posibilidad de evidenciar mayor apropiación del
concepto matemático. Manifestación de dudas
en la verbalización y presencia de silencios por momentos; se reconoce en casos como: “No, no sé qué
decir”; “Pues… yo diría que, para muchas cosas, pero esas muchas cosas no las sabría decir”;
“A ver, como ya estamos con
otra cosa, entonces a ver yo me acuerdo porque… ósea, número entero no es que
más o menos, algo así, entonces a veces también depende del clima, las horas
que uno, ósea que maneja
en el automóvil, no sé qué más, kilos de café, eso mis familias
emplean eso en los
kilos de café o algo así.”
Otras categorías que hacen parte del estudio se enuncian
a continuación, cuyo desarrollo se encuentra dentro de la tesis: Falta de
atención; Presión (tiempo); Resistencia; Memoria; Papel del maestro.
En este orden de ideas, se concluye la existencia de
múltiples condiciones que inciden en la presencia de una posible dificultad de
aprendizaje respecto al número entero, condiciones que generalmente no son
percibidas por maestros e incluso por los mismos estudiantes. Es preciso actuar ante la identificación de tales dificultades, hecho que dependerá
del motivo o motivos que le
generan puesto que podrían definirse, en términos generales, como condiciones
internas o externas de quien aprende y que atienden de manera simultánea a los
procesos de ensañanza y aprendizaje.
REFERENCIAS BIBLIOGRÁFICAS
•
Campos Arenas, A. (2005). Mapas
conceptuales, mapas mentales y otras formas de representación del conocimiento.
Bogotá: Editorial Magisterio.
•
Claxton, G. (2001).
Aprender. El reto del aprendizaje continuo. España: Editorial
Paidós.
•
Hernández Sampieri, R., Fernández Collado, C., &
Baptista Lucio, P. (2010).
Metodología de la Investigación (5ta. ed.). México D. F.: Mc Graw Hill.
•
Minayo, M. C. (2010).
Los conceptos estructurantes de la investigación cualitativa. Salud
colectiva, 251-261.
•
San Martin Cantero, D. (2014). Teoría fundamentada y Atlas.ti: recursos
metodológicos para la investigación educativa. Revista Electrónica de
Investigación Educativa, 104 - 122.
•
Schunk, D. H. (2012). Teorías del aprendizaje. Una perspectiva
educativa. México: Pearson Educación.
•
Strauss, A., & Corbin, J.
(2016). Bases de la investigación cualitativa: técnicas y procedimientos para
desarrollar la teoría fundamentada. Colombia: Universidad de Antioquia.
•
Trindade, V. A. (2016). Entrevistando en investigación cualitativa y los
imprevistos en el trabajo de campo: de
la entrevista semiestructurada a la entrevista no estructurada. En Técnicas y
estrategias en la investigación cualitativa (págs. 18 - 34).
•
Varguillas, C.
(2006). El uso de atlas.Ti y la creatividad del investigador en el análisis
cualitativo de contenido upel. Instituto pedagógico rural el mácaro. Laurus, 72
- 87.
ORATORES ISSN
Impreso: 2410-8928 ISSN Electrónico: L-2644-3988. Número 17. Diciembre 2022 -
Mayo 2023