CATEGORIZACIÓN DE DIFICULTADES ASOCIADAS AL APRENDIZAJE DE LOS NÚMEROS ENTEROS

Diego Alejandro Cruz Echeverri Universidad UMECIT, Panamá Correo: profedace2009@hotmail.com ORCID ID: https://orcid.org/0000-0001-6888-5245

DOI: 10.37594/oratores.n14.537

Fecha de recepción: 08/03/2021 Fecha de revisión: 24/04/2021 Fecha de aceptación: 13/05/2021

RESUMEN

Dentro de los procesos de aprendizaje en el área de matemáticas, es posible que hayamos tenido dificultades originadas por diversos aspectos, por ejemplo, por la no comprensión del concepto trabajado, temor a equivocarnos o hablar en público, conflictos para verbalizar, aprietos con la memoria, alguna condición cognitiva, disgusto o apatía por las propias matemáticas, y así por el estilo otras razones que se puedan citar, sin embargo, no es posible que estas dificultades tengan la misma naturaleza, percibiendo en mi experiencia como docente que algunos estudiantes reflejan durante la práctica comprensión de los conceptos, pero en la presentación de pruebas escritas no reflejan los mismos desempeños, por ejemplo. No debe entonces normalizarse el uso del término “dificultades de aprendizaje” para catalogar estudiantes, con el desconocimiento de lo que antecede a una manifestación que pueda dar indicios de ello y más cuando existe la posibilidad que no lo sea. En el recorrido de este estudio, se realiza el rastreo de algunas investigaciones referentes al tema en mención, procurando hacer claridad en lo que es el aprendizaje y algunas de sus facultades, de acuerdo con Claxton (2001) y Schunk (2012) principalmente, el conocimiento matemático, sobre dificultades de aprendizaje en matemáticas y finalmente, en el tema de la evaluación, centrando la atención en el concepto matemático referente a los números enteros, en correspondencia con el grado séptimo de educación básica secundaria.

Palabras clave: matemáticas, aprender, dificultad de aprendizaje, naturaleza, recursos internos y externos, evaluación, número entero.

CATEGORIZATION OF DIFFICULTIES ASSOCIATED TO THE LEARNING OF THE WHOLE NUMBERS

ABSTRACT

Within the processes of learning in the area of mathematics, it is possible that we have had difficulties originated by diverse aspects, for example, by the nonunderstanding of the worked concept, fear to be mistaken or to speak in public, conflicts to verbalize, jams with the memory, some cognitive condition, misfortune or apathy by the own mathematics, and thus of the sort other reasons that can be mentioned, nevertheless, he is not possible that these difficulties have the same nature, perceiving in my experience like educational that some students reflect during the practical understanding of the concepts, but in the presentation of written tests they do not reflect performances such, for example. The use of the term does not have then to be standardized “learning difficulties” to catalogue students, with the ignorance of which it precedes to a manifestation that can give indications of it more and when the possibility exists that is not it. In the route of this study, the tracking of some referring investigations to the subject in mention is made, trying to make clarity in which it is the learning and some of its faculties, in agreement with Claxton (2001) and Schunk (2012) mainly, the mathematical knowledge, on difficulties of learning in mathematics and finally, in the subject of the evaluation, centering the attention in the mathematical concept referring to the whole numbers, in correspondence with the degree seventh of secondary basic education.

Keywords: mathematics, learn, difficulty of learning, nature, resources internal and external, evaluation, whole number.

INTRODUCCIÓN

Algunos estudios sobre dificultades relacionadas con el aprendizaje de las matemáticas

En el contexto colombiano, el proceso educativo en el área de matemáticas está orientado por varios textos propuestos desde el Ministerio de Educación Nacional denominados referentes de calidad, entre los que se encuentran: los Lineamientos Curriculares de Matemáticas, los Estándares Básicos de Competencias en Matemáticas y los Derechos Básicos de Aprendizaje junto a la Matriz de Referencia, en los que se detallan orientaciones referidas a las competencias que se deben trabajar y desarrollar en los estudiantes, por ciclos, en relación con los cinco pensamientos matemáticos y a su vez, los cinco procesos generales a cada uno de ellos (MEN, 1998), los cuales se relacionan a continuación:

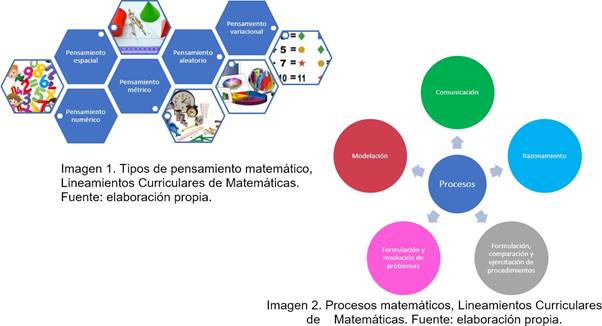
Además, en correspondencia con estos componentes, se hace necesario explicitar los tres contextos planteados en el aprendizaje de las matemáticas: contexto inmediato o de aula, contexto escolar o institucional y contexto extraescolar o sociocultural (MEN, 1998). Desde esta perspectiva, el contexto no necesariamente hace refencia a un lugar físico, sino más bien, en un sentido sociocultural, a un conjunto de componentes que caracterizan una población, tal como lo explicita el MEN (1998), en el cual se construye sentido y significado de lo que se enseña/aprende.

Lo anterior, para señalar algunos elementos fundamentales en relación con la enseñanza y aprendizaje de las matemáticas, en su conexión con la posibilidad de identificar dificultades en el aprendizaje de las matemáticas y reconocer la naturaleza asociada a ellas. Al respecto, son diversos los estudios e investigaciones que se han realizado acerca de dificultades asociadas al aprendizaje de las matemáticas, siendo posible citar, entre algunos otros, a Duval (2016), Hudson (2017), Inostroza (2018), Palencia (2019) y Romero (2004), de tal manera que varios de ellos se refieren a dificultades pero se hace necesario pensar en su identificación y clasificación, situaciones que conducen a considerar el sentido e implicaciones que tienen desde la posibilidad de identificar y comprender su naturaleza, en la búsqueda de establecer una categorización de las mismas, dadas las circunstancias que como docentes de matemáticas vivimos en el aula, y a las que se ven enfrentados los estudiantes, las cuales se tienen al momento de identificar un estudiante con posibles dificultades de aprendizaje en el área y, ante un abanico de posibilidades frente a su naturaleza; por tanto, categorizar dichas dificultades favorecería la atención previo conocimiento de su naturaleza.

Así, por ejemplo, en su estudio, Sepúlveda, Opazo, Díaz-Levicoy, Jara, Saéz y Guerrero (2016) corroboraron tres marcos específicos para explicar la dificultad de aprender matemática: de un lado, las que emergen por la propia naturaleza de las matemáticas, por otro lado, las ocasionadas por el profesor, directa o indirectamente y, finalmente, aquellas originadas por condiciones propias del estudiante. Textualmente, afirman que “la dificultad de aprender matemática no es el resultado de un único factor sino, más bien, es una combinación y acumulación de varias razones siendo las principales, según los alumnos, aquellas originadas por el propio estudiante” (p. 105), realizando una aproximación pero no dejan ver una caracterización de las dificultades, tampoco vislumbran una manera que permita su identificación, o establecer similitudes o diferencias entre ellas a partir de posibles regularidades, aspectos que se tornan de interés para la presente investigación dado que se hace referencia a elementos que se asocian tanto de manera externa como interna con el estudiante.

De otro lado, se identifica que Inostroza (2018) presenta hallazgos correspondientes con los planteamientos anteriores, en el sentido que, manifiesta que dichas dificultades corresponden a una condición intrínseca del estudiante, y que su origen está asociado tanto a problemas de salud, como a metodologías inadecuadas de enseñanza de las matemáticas, reconociendo así que las causas pueden ser múltiples y diversas, más no se profundiza en ese sentido, de tal manera, que permita esclarecer si se pueden clasificar dichas dificultades por aspectos comunes entre ellas.

Por su parte, Fonseca, López y Massagué (2019) refieren el cálculo como una de las habilidades más importantes en el trabajo con las matemáticas, reconociéndola además entre las de mayor incidencia en los problemas de aprendizaje de los estudiantes. Con lo anterior, abordan la discalculia en su concepción como trastorno específico del aprendizaje de las matemáticas, cuyos indicios pueden evidenciarse en conflictos con la concepción del número, la seriación, operaciones que conllevan al cálculo mental y la solución de situaciones problema, carentes de confianza y que procuran evitar actividades relacionadas con números. Así, concluyen su estudio resaltando la importancia de analizar dicha dificultad y sus síntomas, en cuanto permite a los maestros estar preparados para su atención desde la prevención, corrección y/o compensación. Es así como la falta de criterios para la identificación de dificultades y, la multiplicidad de factores involucrados en el aprendizaje de las matemáticas, conducen a pensar si es posible hacer una categorización de dificultades en el aprendizaje de las matemáticas, asociadas a su naturaleza, y de esa forma se llega a justificar la necesidad de dicho propósito.

Palencia (2019) realiza una aproximación relacionada con los diferentes elementos que se despliegan en la cultura escolar y que de cierta manera fortalecen creencias, expectativas y consideraciones por parte de los docentes sobre los estudiantes que presentan dificultades en el aprendizaje de las matemáticas. Invita a no naturalizar el referirse a dificultades en el aprendizaje de las matemáticas, pues no pueden interpretarse de la misma forma, igualmente a reflexionar sobre las prácticas evaluativas. De ahí que centra la atención en la necesidad de clarificar la naturaleza de dichas dificultades, y no asumirlas de manera general desde otras teorías, por ejemplo, las clásicas del déficit como él mismo lo señala, sin embargo, no se hace ningún tipo de claridad sobre tal elemento ni se proporcionan indicios que permitan su identificación o reconocimiento, o de qué manera se podrían agrupar dichas dificultades.

Duval (2016), por su parte, inicia su artículo con varios interrogantes, uno de los cuales y por razones explícitas llama la atención es “¿Cuál es la naturaleza de estas dificultades?” (p. 61), haciendo referencia precisamente al aprendizaje de las matemáticas. Plantea, entre otras cosas, que tenemos un desafío educativo y a la vez teórico para investigar sobre el desarrollo y el aprendizaje de las matemáticas. Así mismo, esboza un interrogante en relación a investigación en el aprendizaje de las matemáticas y las dificultades que se le relacionen, cuestionándose acerca de “¿cómo podemos analizar los procesos de adquisición de conocimiento a partir de las concepciones de los estudiantes y encontrar las fuentes de sus dificultades?” (p. 62), esto al reconocer que tales investigaciones se deberían fundamentar en lo que hacen los estudiantes, en lo que producen y dicen. Dado que son diversas las formas de aprender y, en consecuencia, las dificultades que ello puede conllevar, así como la causa que les motiva, cobra importancia la presente investigación dado que tales aspectos podrían profundizarse en un estudio que permita esclarecer la naturaleza de dichas dificultades.

¿Dificultades en el aprendizaje de las matemáticas?

Ahora bien, deben notarse las dificultades que a lo largo de la historia se han presentado en el aprendizaje de las matemáticas, situación que no es ajena a la realidad. Desde la experiencia como estudiante se tuvo la posibilidad de conocer casos de personas que presentaban dificultades para el aprendizaje de las matemáticas, puesto que así lo asumían ellos mismos, aun teniendo claro que son necesarias e importantes en diversos contextos y situaciones de la vida, y las razones de ello podrían ser diversas. Por otro lado, ahora como docente de matemáticas, me han llamado la atención casos de estudiantes que, por más que se esfuerzan y lo intentan, continúan presentando manifestaciones de posibles dificultades, desconociendo cuáles pueden ser los motivos por los cuales ellos no han logrado consolidar su aprendizaje en el área.

Con lo anterior, en el campo de una ciencia exacta como lo son las matemáticas, se amplía el panorama frente a la diversidad de posibles dificultades que evidencian los estudiantes durante los procesos de aprendizaje y su respectiva naturaleza y, en general, en su proceso de formación,

sentido en el cual llama la atención la relación de éstas con el papel de los docentes en las clases, y con las posibles dificultades a las que se pueden ver enfrentados los estudiantes desde los primeros años de escolaridad, reconociendo que dichos estudiantes pueden ser más competentes en otros campos o áreas de conocimiento. También es importante mencionar que las características del conocimiento matemático pueden llevar a que el estudiante tenga dificultades, hay estudiantes con mucha habilidad para resolver cálculos mentales, pero a la hora de resolver ecuaciones algebraicas presentan dificultad.

De acuerdo con Hudson (2017), es común que una dificultad de aprendizaje se repita en una misma familia, pero además se producen en todos los grupos raciales y contextos económicos, sin establecer distinción alguna sobre ellos. Afirma también que no es posible curar tales dificultades ni mucho menos desaparecerlas, lo que no se convierte en una condena puesto que se debe buscar la manera de contribuir a su superación en la búsqueda de personas competentes, aspecto en el que los maestros jugamos un papel importante. Por tal motivo, se considera necesario debatir procesos que permitan la identificación de dichas dificultades, a razón de poder comprenderlas y proponer una categorización de ellas, de acuerdo a la naturaleza de las mismas. De otro lado, podemos referirnos a aquellas experiencias de aprendizaje que generan aparentes dificultades, tal vez por equivocaciones en momentos específicos que conllevan a fristraciones o temores, que impiden al estudiante intentarlo nuevamente.

De acuerdo con la Real Academia Española, se concibe a la dificultad como la oposición o contrariedad que impide conseguir, ejecutar o entender algo bien y pronto, mientras que Schunk (2012) la asume como el hecho que revela lo que uno puede y no puede hacer. De otro lado, éste último afirma que “aprender implica construir y modificar nuestro conocimiento, así como nuestras habilidades, estrategias, creencias, actitudes y conductas” (p. 2), haciendo referencia a lo que es el aprendizaje, y del cual se extraen posibles categorías para referirnos a dificultades: dificultades en las habilidades, dificultades en las estrategias, dificultades en las creencias, dificultades en las actitudes, dificultades en las conductas, dificultades en los procedimientos, dificultades en los conocimientos. Por otro lado, partiendo de los conceptos de dificultad y aprendizaje, Romero & Lavigne (2004) afirman que:

Las Dificultades en elAprendizaje se refieren a un grupo de trastornos que frecuentemente suelen confundirse entre sí. Las razones fundamentales de tal confusión son: la falta de una definición clara, los solapamientos existentes entre los diferentes trastornos que integran las Dificultades en el Aprendizaje, sobre todo cuando median aspectos de privación educativa y social, y, en tercer lugar, la heterogeneidad de la población

escolar a la que se refieren. (p. 7)

De esta manera, se plantea la posibilidad de que dichas dificultades se asocien a trastornos del aprendizaje que afectan la correcta adquisición y ejecución de diferentes habilidades matemáticas, como por ejemplo, la estimación, el cálculo mental, la medición, el análisis de datos, la visualización espacial, al concluir en la carencia de una estructuración mental que posibilite el aprendizaje, enmarcado a partir de los procesos propuestos desde los Lineamientos Curriculares (1998) y Estándares Básicos de Competencias de matemáticas (2006): formular y resolver problemas; modelar procesos y fenómenos de la realidad; comunicar; razonar, y formular, comparar y ejercitar procedimientos y algoritmos. (p.51). Desde esta perspectiva y aludiendo a la multiplicidad de dificultades que pueden presentar los estudiantes, y que en algunos casos se pudiera llegar a la subjetividad, se encuentra una relación con Romero & Lavigne (2004), quienes sostienen como uno de los principios de partida que:

Las Dificultades en el Aprendizaje son un fenómeno verdadero, no una invención, ni una construcción social. A pesar de los condicionantes psicológicos, educativos, políticos, ideológicos y filosóficos implicados en su aparición, y sobre todo, en su extraordinario desarrollo, de los más que aparentes intereses profesionales y familiares; y a pesar de los problemas existentes para definir adecuadamente las Dificultades en el Aprendizaje, es un hecho que existe un importante número de alumnos con problemas para aprender las tareas escolares, que no se deben a causas sensoriales, a privaciones crónicas ni a graves discapacidades intelectuales. (p. 9-10)

En este sentido, reconociendo la presencia real de dificultades en el aprendizaje y la multiplicidad de posibles causas, concretamente en relación a las matemáticas, referidas con antelación, debe atenderse a ellas de tal manera que tanto maestros como estudiantes seamos conscientes de ello, y en esa misma medida se puedan atender a partir del reconocimiento de su naturaleza, así como el médico atiende y trata a su paciente previo conocimiento del origen de su molestia, es una realidad que no debe sub ni sobrevalorarse.

De otro lado, Hudson (2017) presenta la siguente acotación:

Las estimaciones sugieren que, en una clase típica de unos 30 alumnos, habrá uno, o probablemente dos, alumnos con una Dificultad Específica de aprendizaje (DEA). Se encuentran en todo tipo de escuelas y presentan diversos niveles de discapacidad. Desafortunadamente para algunos de estos alumnos, a lo largo de toda su vida escolar, no se identificará cuál es su particular dificultad de aprendizaje y, por tanto, se encontrarán desprovistos de apoyo. Puede que hasta su inteligencia y su potencial sean infravalorados. Existe incluso el peligro de que abandonen la escuela con una baja autoestima y unas calificaciones y aspiraciones de futuro inferiores a las que podrían alcanzar. (p. 9)

Por consiguiente, se proporciona sustento a lo enunciado cuando dichas dificultades son una realidad latente, que en ocasiones se prefiere hacer caso omiso, por diferentes razones, en el caso propio una de ellas puede corresponder al desconocimiento e incapacidad para identificarlas, sin pensar en las consecuencias a corto, mediano y largo plazo. Es así como durante los procesos de enseñanza se observan dificultades, en algunos estudiantes, para alcanzar los niveles esperados en el área, lo que genera y despierta el interés por analizar la naturaleza de ellas en los casos que un estudiante no responde acorde con las características de un concepto en correspondencia con las propiedades matemáticas. Lo anterior conduce, por lo general, a un juzgamiento a priori sin analizar qué puede suceder tras cada situación, siendo posible que como maestros desconozcamos las razones y causas, y más aún, se propongan alternativas metodológicas sin saber realmente cuál es el origen de la dificultad.

De esta manera, en el reconocimiento de la presencia de dificultades de aprendizaje referidas a las matemáticas por parte de algunos estudiantes, en la necesidad de intervenir y actuar frente a ellas, en los bajos resultados obtenidos para el área tanto en pruebas internas como externas, en las experiencias vividas día a día en las aulas de clase con cada uno de ellos, dado que no se vislumbra claramente la naturaleza de las dificultades, no hay suficiente claridad y es de interés para la comunidad, no sólo educativa, es imperante generar estrategias que contribuyan, en primera medida, a su identificación como dificultades y la naturaleza de las mismas, elemento que se considera de gran relevancia en el presente proceso de investigación, situación que se espera permita y favorezca la categorización de las mismas para un posterior tratamiento, a partir de la cual se genera la siguiente pregunta de investigación: ¿De qué manera se pueden categorizar dificultades en el aprendizaje de números enteros a partir de su posible naturaleza?

Posteriormente, en el ejercicio de reconocer la presencia de dificultades en el aprendizaje de las matemáticas, referidas al concepto de número entero, se configura la necesidad de identificarlas y categorizarlas teniendo en cuenta su naturaleza y características, desde diferentes miradas, situación que puede conducir, desde la práctica, al pensar en “cómo enseñar” (maestro) más que en “cómo aprender” (estudiantes), especialmente aquellos que son sujetos a una o varias dificultades en el aprendizaje.

Pero… ¿Qué es el aprendizaje?

Aprender implica la construcción y modificación del conocimiento, igualmente de habilidades, estrategias, creencias, actitudes y conductas (Schunk, Teorías del aprendizaje. Una perspectiva educativa, 2012), lo que indica que cuando una persona aprende no puede ser la misma que era antes, y en efecto, así debe ser, pero ¿cómo medir o hacer evidentes dichos cambios? ¿Sería posible, entonces, afirmar que una persona que no aprende sigue siendo la misma en cuanto a la definición anteriormente dada? Ya que, si tenemos presente la posibilidad de aprender habilidades desde lo cognoscitivo, lingüísticas, motoras y sociales, de acuerdo con él mismo, también es posible que dichas habilidades tomen muchas formas, razón por la cual no sería posible estandarizar tal medida.

En cuanto a teorías del aprendizaje, tema en cuestión, se tiene que filósofos como Platón, René Descartes y Emmanuel Kant, precursores del racionalismo, propusieron el uso de la razón en lo que al conocimiento concierne. Este último, por su parte, reafirmó el papel de la misma como la fuente del conocimiento, que a su vez opera dentro del campo de la experiencia, en el sentido que el conocimiento absoluto no existe sin la influencia del mundo externo. Se sostiene que la información se toma del mundo, pero es la mente la encargada de interpretarla (Schunk, 2012), elementos que coinciden, en cierta medida, con lo planteado en los Estándares Básicos de Competencias en Matemáticas (MEN, 2006), en lo referido al conocimiento formal e informal, y las relaciones y conexiones que se pueden establecer entre ambos. La razón (mente) desempeña un papel fundamental en el ejercicio de aprender, no es posible desconocerlo, más aún cuando desde la neurociencia se investigan los diferentes procesos que se llevan a cabo al interior del cerebro.

Estructura del pensamiento (cognitivo)

Para Claxton (2001), “el cerebro está construido para llevar a cabo ciertos tipos de aprendizaje con una brillantez que puede verse perturbada fácilmente si se piensa demasiado y si se intenta con demasiada intensidad” (p. 19). De otro lado, argumenta que el intelecto nos proporciona diversas herramientas perfeccionadas que desempeñan un papel importante para el aprendizaje, por ejemplo, el conocimiento, en relación a la acumulación de datos e información; las destrezas, como lo es el aprender a utilizar las TIC; así mismo como las diferenciaciones, las preferencias, las disposiciones y el carácter. Es así, como lo afirma, que el aprendizaje no sólo logra cambiar nuestro conocimiento y nuestro hacer, sino que también lo hace con nuestro ser, y por esa razón es que el aprendizaje es continuo.

De acuerdo con el mismo autor, la capacidad natural para aprender que posee el cerebro puede aumentar, transformar y administrarse de diversas formas. De un lado, se tiene el desarrollo y evolución biológica, y de otro, el desarrollo de la cultura, a través de los cuales se genera una

serie de capacidades para aprender, bien llamadas cajas de herramientas al hacer referencia al conjunto de recursos internos y externos dispuestos para la función del aprendizaje.

Un elemento a considerar es el de la memoria, en la medida que es un tema discutido y debatido a lo largo de la historia en relación a su uso y el papel que desempeña durante y después del aprendizaje, sentido en el que se destacan las teorías cognoscitivas que comparan el aprendizaje con el almacenar en la memoria conocimiento organizado y significativo, es decir, con la codificación (Schunk, Teorías del aprendizaje. Una perspectiva educativa, 2012). En relación a ella, el autor plantea que

La información se recupera de la memoria en respuesta a claves relevantes que activan las estructuras apropiadas de la memoria. El olvido es la incapacidad de recuperar la información de la memoria debido a la interferencia, la pérdida de la memoria o a claves inadecuadas para acceder a ella. La memoria es fundamental para aprender, y la forma en que se aprende la información determina cómo se almacena y se recupera. (p. 23)

Partiendo de lo anterior, se ponen en consideración elementos relacionados con la memoria para la presente investigación, con el ánimo de determinar la relación e influencia que puede ejercer la memoria en asociación a dificultades en el aprendizaje de las matemáticas, dada la dificultad que conlleva para algunas personas, en su papel de estudiantes, el recuperar información necesaria.

Schunk

El aprendizaje es para Schunk (2012) “un cambio perdurable en la conducta o en la capacidad de comportarse de cierta manera, el cual es resultado de la práctica o de otras formas de experiencia” (p. 3), coincidiendo en parte con los Estándares Básicos de Competencias en Matemáticas (MEN, 2006), en cuanto al conocimiento informal y formal. Además, plantea que el aprender implica un cambio, como ya se ha mencionado antes, perdura a lo largo del tiempo y ocurre por medio de la experiencia, elemento último que considero de gran importancia, más aún en el aprendizaje de las matemáticas, cuando se supone partimos de lo concreto para llegar a la abstracción, pero en la medida de lo posible, permitiendo la experimentación, ya que podría decirse que no es igual aprender viendo, que aprender haciendo. Aclara, también, que el aprendizaje es algo inferencial, ya que no es posible observarlo directamente, sólo a través de productos o resultados que se puedan obtener de los estudiantes, de ahí la necesidad de utilizar diversos métodos e instrumentos de evaluación, y no limitarse únicamente a una prueba escrita para determinar si en un estudiante hubo aprendizaje o, por el contrario, se encuentra ante la posible presencia de alguna dificultad de aprendizaje.

También hace referencia a algunos temas que han llamado la atención de investigadores en relación al aprendizaje, como lo son la motivación, la tecnología y la autorregulación, siendo posible, en este punto, establecer una correlación con la propuesta de Claxton (2001) en cuanto a los recursos internos y externos para el aprendizaje, haciendo parte de estos últimos la tecnología, en la medida que hace que el aprendizaje esté supeditado a los medios que se utilizan, por ejemplo, no será lo mismo aprender a realizar algunas construcciones geométricas con regla y compás que haciéndolo con Geogebra; a nivel de los recursos internos, pensaría en la autorregulación como un elemento clave para la consolidación del aprendizaje mismo y que pudiera convertirse en una categoría importante dentro de la presente investigación, en referencia a las habilidades cognitivas.

Claxton

De acuerdo con Claxton (2001), aprender forma parte de nuestra naturaleza como seres humanos, dado que durante el aprendizaje se logra moldear la mente y los hábitos para adaptarse al mundo. Contrario a algunas creencias, el aprendizaje no es esencialmente intelectual, afirma, y al respecto menciona que lo que sucede en escuelas y universidades con las orientaciones de los profesores es sólo una clase de aprendizaje.

De la misma forma, se reconoce que el aprendizaje no es una actividad homogénea, razón por la que, desde la experiencia, se observa que las personas poseen diferentes formas para aprender, igualmente sucede en diferentes tiempos y en diversos niveles, algunas aprenden con mayor facilidad que otras y empleando más, o menos, recursos. En relación a lo anterior, sostiene que “hay muchas personas que, al encontrar algo difícil, piensan que eso significa que carecen de inteligencia, y no que, simplemente, no han desarrollado aún, o recuperado, la herramienta de aprendizaje adecuada.” (Claxton, 2001, p. 18), del mismo modo que se encuentra la posibilidad de que para una persona el aprendizaje sea bloqueado por falta de confianza en sí misma, por miedo al fracaso o la humillación, condiciones que hacen referencia a la resistencia, una condición para el aprendizaje, como podría suceder en algunos casos.

El autor afirma que en general, “las personas […] difieren enormemente en cómo aprenden y en lo bien que lo hacen” (p. 13), tanto en estilo como en eficacia, y esto empieza a suceder muy pronto. Sostiene también que dichas diferencias son suceptibles a modificarse a lo largo de la vida, y un elemento importante en su discurso, que bien vale la pena tener presente, es el siguiente: “El desarrollo de la resistencia frente a la incertidumbre y la dificultad […]” (p. 14) es uno de los ejes principales para fomentar el buen aprendizaje, oportuno y apropiado al hacer referencia a dificultades en el aprendizaje. Plantea entonces lo que ha denominado las tres R del aprendizaje:

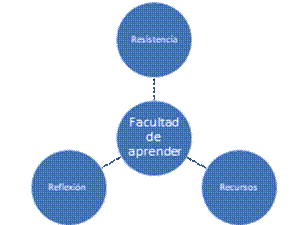
Imagen 3. Aprender - El reto del aprendizaje continuo. Claxton (2001) Fuente: elaboración propia.

Es importante tener presente que la facultad para aprender se desarrolla, así como también es posible evitar los bloqueos, en la presencia de condiciones adecuadas, sostiene Claxton (2001). Esto quiere decir que, frente a una posible dificultad de aprendizaje, con claridad frente a su naturaleza, es posible planear intervenciones en cuanto se diseñen los ambientes, estrategias y recursos adecuados, lo cual va ligado a la misma naturaleza. De ahí la importancia y necesidad de la presente investigación.

Señala, además, cuatro elementos importantes de la caja de herramientas del aprendizaje: el primero de ellos corresponde a la inmersión, siendo un tipo de aprendizaje centrado en el mundo físico, mayoritariamente de carácter social y debido a ello implica elementos como la interacción y la imitación, que a su vez permiten la comunicación de habilidades prácticas. Los otros tres elementos corresponden a la imaginación, las habilidades intelectuales y la intuición.

Dificultades de aprendizaje

Fernández Carreira (2003) afirma que actualmente no existe una definición universal referente a dificultades del aprendizaje, enfatizando en la importancia de abordarlas desde sus causas, con la intensión de prevenirlas, de ser posible en los primeros años de escolaridad, al poder identificarlas para su posterior tratamiento.

Así mismo, Claxton (2001) hace referencia a una función conjunta entre recursos internos y externos para el aprendizaje, en la medida que para ser buen aprendiz se requiere saber reconocer las ventajas y posibilidades que puede traer cualquier situación, pero además debe hacerse un buen uso de ellas. Debe poseerse la habilidad para idear los medios o poseer el ingenio práctico, pero también se requiere de recursos internos bien desarrollados, razones por las que la facultad de aprender no recide únicamente en la mente, dada la convergencia y complementariedad de ambos recursos, internos y externos, situación que puede aplicar también al momento de identificar una dificultad de aprendizaje, en cuanto se hace necesaria la identificación y reconocimiento de su naturaleza.

En el caso concreto, Hudson (2017) señala las siguientes dificultades de aprendizaje: Dislexia, Discalculia, Disgrafía, Dispraxia, Trastorno por Déficit de Atención e Hiperactividad (TDAH), Trastorno del Espectro Autista (TEA) y Síndrome de Asperger, Trastorno Obsesivo Compulsivo (TOC), habilidades organizativas en relación a otras dificultades de aprendizaje, siendo la discalculia una dificultad de aprendizaje específica de las matemáticas.

Dificultades en el aprendizaje de las matemáticas

Una de las más conocidas y mencionadas es la discalculia. Hudson (2017) la compara con la dislexia, pero en este caso sucede con los números; se le entiende como dificultades con el cálculo y la aritmética, y de acuerdo con el Department for Education and Skills (2001, citado en Hudson, 2017) se define como “una afección que afecta la habilidad para adquirir competencias matemáticas” (p.47), de tal manera que no se limita únicamente al cálculo y la aritmética, sino que se extiende a las matemáticas en general, es decir, a los cinco pensamientos y sus respectivos procesos, de los cuales ya se hizo mención. Al respecto, se reconoce su presencia en al menos un 5% de la población, pero se manifiesta además la posibilidad de que un número mayor la tenga en combinación con otras dificultades de aprendizaje.

Tal como se ha indicado, es probable que la discalculia posea componentes genéticos, en cuanto a través de estudios se ha comprobado su repitencia dentro de una misma familia (Hudson, 2017), coincidiendo con Blakemore & Frith (2008), quienes afirman igualmente que la discalculia es un problema que se hereda de familia; es importante señalar, además, que no existe una cura para la misma. Es común, por tanto, encontrar en las aulas estudiantes que de una u otra forma muestran rechazo, apatía, disgusto hacia las matemáticas, no se les da, y lo que se trata de precisar es la razón o naturaleza de ello, puesto que no es posible generalizar o simplemente decir que tienen discalculia.

De acuerdo con Hudson (2017), es probable que un estudiante con discalculia tenga dificultades para recordar un número de teléfono, que carezca de confianza ante las matemáticas y por lo tanto trate de evitar actividades que las involucren. Señala, en relación a los números, que estos estudiantes no cuentan con la habilidad para captarlos intuitivamente; en relación a la comprensión de enunciados escritos, tienden a entrar en pánico y bloquearse con preguntas que hagan referencia a los números, en especial cuando se hace bajo presión; desde la memoria a corto plazo, se les dificulta recordar los números con los que hay que trabajar durante los cálculos al igual que series e instrucciones; en la representación gráfica, puede ser un problema para ellos el llegar a tiempo a algún lugar o saber qué hora es.

Se reconocen así, primero, la multiplicidad de posibilidades al referirse a causas (naturaleza) de dificultades asociadas al aprendizaje de las matemáticas, y segundo, la importancia de conocerlas, en cuanto ese conocimiento posibilita la atención de las mismas de acuerdo a sus características y condiciones específicas. En ese orden de ideas, concuerda Dehaene (2016) con Blakemore & Frith (2008) al afirmar que “es muy probable que muchos de los que muestran dificultades con la aritmética no tengan ningún daño biológico” (p.399) y sugiere, por ejemplo, que no se les ha enseñado bajo métodos apropiados. Dehaene (2016) plantea la posibilidad de que estas dificultades sean agravadas por componentes emocionales, ansiedad creciente o fobia a las matemáticas. El propósito de la presente investigación no busca su atención, sino el brindar los conocimientos frente a su naturaleza, los cuales podrán ser retomados por otros investigadores posteriormente.

Concepto matemático de número entero

Desde la antigüedad, el hombre se ha visto enfrentado a la necesidad de resolver problemas y en esa misma medida ha intentado encontrarles solución, el origen del conjunto de los números enteros no es ajeno a dicha realidad. Su historia se remonta a la India, cuyos primeros indicios se encuentran en el libro de un matemático hindú, Brahmagupta, en el que se hace una distinción entre bienes, deudas y nada, términos con los que se hace referencia a los números positivos, los negativos y el cero, respectivamente (Ortiz, y otros, 2013); posteriormente se identifican otros aportes en la construcción y consolidación del concepto, los cuales datan entre los años 628 y 1850 d. C., como se muestra en la siguiente imagen:

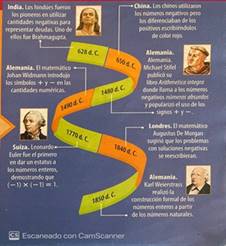
Imagen 4. Cronología de números enteros. Fuente: Los Caminos del Saber Matemáticas 7, p. 9

Son diversas las aplicaciones de los números enteros en la vida diaria y, en general, de las matemáticas, razón por la que se tienen presentes tanto los aprendizajes que se formalizan en el aula de clase como los que se obtienen de manera empírica, sentido en el que se considera importante la vinculación entre ambos. Algunas de esas aplicaciones se encuentran al referirse a ganancias y pérdidas, altura y profundidad sobre el nivel del mar, variaciones en la temperatura, desplazamientos hacia arriba, abajo, izquierda o derecha (plano cartesiano), etc., de tal forma que ahora es posible, por ejemplo, sustraer una cantidad mayor de una menor, lo que no se podía hacer antes de la introducción de dicho concepto y que podría generar resistencia o confusión en algunos estudiantes, tal como he podido notar en mi experiencia como docente.

Propiamente, en el sistema educativo colombiano, de acuerdo a los Estándares Básicos de Competencias en matemáticas (MEN, 2006), la enseñanza inicial de este concepto, y lo relacionado a él, se da entre los grados sexto y séptimo de educación básica secundaria, teniendo en cuenta que ambos grados hacen parte del mismo ciclo y, dentro de la autonomía conferida a cada institución educativa, se realiza la respectiva distribución dentro de estos dos grados. A continuación, se toma como ejemplo el plan de formación asumido en la institución donde actualmente laboro, en el que se identifica la subdivisión asumida para la enseñanza del número entero a partir de su identificación.

Imagen 5. Plan de formación para el grado séptimo, en relación al concepto matemático de número entero.

Se observa cómo del concepto de número entero se desprenden otros en relación a él, los cuales se complementan con un concepto anterior, el conjunto de los números naturales. Es precisamente la transición entre ambos conjuntos numéricos la que llama la atención, pues de su correcta comprensión y aprendizaje depende, en cierta medida, el éxito o fracaso en los siguientes grados de escolaridad, por llamarlo así, dado que a partir del grado séptimo este concepto se aplica en los demás contenidos propuestos en el plan de formación respectivo a cada grado, y aún después

del colegio en la universidad, y como mencioné en párrafos anteriores, sin perder de vista su aplicabilidad en la vida diaria.

Evaluación del aprendizaje en matemáticas

Un factor a considerar en todo este asunto del aprendizaje, es el referido a la evaluación, en cuanto a la necesidad de comprobar si un estudiante efectivamente aprendió o no, pero partiendo del hecho que no es posible observarlo de manera directa. Sin embargo, en nuestra cultura, la prueba escrita es uno de los medios directos para verificarlo, puesto que así también lo considera Schunk (2012) al afirmar que “a menudo el aprendizaje se evalúa a partir de los exámenes escritos de los alumnos mediante pruebas, cuestionarios, tareas, trabajos finales e informes” (p. 15), sin que ello sea garante unánime del proceso como tal, queriendo decir que no necesariamente quien responde correctamente el 100% de la prueba es porque en esa medida logró aprender, igualmente con quien no lo logra, no quiere decir estrictamente que no aprendió, pues existen diversos factores que directa o indirectamente ejercen influencia. Tal como lo manifiesta Schunk (2012), para que el investigador o profesional, para este caso el maestro, pueda saber si ha ocurrido el aprendizaje, o no, existen otros procedimientos además de las pruebas, con los cuales es posible obtener la evidencia deseada.

Uno de estos procedimientos, a los que hace referencia, es la observación directa, que consiste en observar los comportamientos que pueden asumir los estudiantes para identificar posibles cambios en ellos, y la cual es comúnmente utilizada por los maestros al interior de las aulas de clase, no siempre para verificar si ha ocurrido aprendizaje o no, señalando que

La observación directa es un índice válido del aprendizaje si las observaciones son claras e implican poca inferencia por parte del observador, y funciona mejor cuando se especifica la conducta esperada y después se observa a los estudiantes para establecer si sus conductas se ajustan al estándar. (p. 14)

Se trata entonces de ser objetivos, en tanto la rigurosidad que amerita la investigación, dejando de lado la subjetividad que conduzca a la inferencia en los comportamientos observados, y como apoyo para tal fin pueden utilizarse las rúbricas, de acuerdo a lo enunciado como, entre otros, un procedimiento de carácter evaluativo.

En relación a lo expuesto hasta el momento sobre lo que es el aprendizaje, Schunk (2012) enuncia algunos procedimientos, de los que se habló en párrafos anteriores para evaluar el aprendizaje:

Imagen 6. Métodos de evaluación del aprendizaje. Tomado de: Schunk (2012), p. 15.

En este punto, se hace claridad frente a que, aunque la observación se contemple como una estrategia en el campo de la evaluación, debe considerarse que sólo se observa lo que es factible de observarse, lo que implica que los procesos cognoscitivos y afectivos que anteceden las acciones de los estudiantes se pasan por alto a través de ella. Señala, además, que:

la ausencia de una conducta apropiada no significa que el individuo no ha aprendido. Aprendizaje no es lo mismo que desempeño, y muchos factores, además del aprendizaje, podrían afectarlo. Existe la probabilidad de que los estudiantes no realicen las acciones aprendidas porque no se sienten motivados, porque se sienten enfermos o están ocupados haciendo otras cosas. (Schunk, Teorías del aprendizaje. Una perspectiva educativa, 2012, pág. 15)

De esta manera, se reconoce la existencia e influencia de diversos factores, internos o externos, durante el aprendizaje, especialmente en el momento de la evaluación, razón por la cual cobra importancia la presente investigación. Lo anterior, dada la posibilidad y, según lo ya enunciado, de que si un estudiante no responde acertadamente según se solicite, no necesariamente quiere decir que no ha aprendido o que se encuentre ante una posible dificultad de aprendizaje, razón por la cual debe conocerse la naturaleza de su accionar, dado que, de acuerdo con Schunk (2012), es necesario descartar dichos factores precisamente antes de concluir que el aprendizaje no ha ocurrido ante la ausencia de determinado desempeño, cuando es común juzgar y determinar el aprendizaje en esa medida, debe trabajarse en su identificación en cuanto que, como se ha venido mencionando,

la presencia de factores extraños pueden llegar a afectar el desempeño y entorpecer el proceso y resultados de la evaluación del aprendizaje. Situación similar sucede con los exámenes orales, el resultado no es del todo confiable puesto que los estudiantes “podrían enfrentar problemas para traducir en palabras lo que saben debido a desconocimiento de la terminología, dificultad para hablar en público o problemas de lenguaje” (p.16), y como las anteriores, es posible que existan otros elementos que interfieran al obtener una respuesta, producto de la evaluación.

Por su parte, en los Estándares Básicos de Competencias en Matemáticas (MEN, 2006) se hace referencia a la evaluación formativa, señalando que debe ponerse “énfasis en la valoración permanente de las distintas actuaciones de los estudiantes cuando interpretan y tratan situaciones matemáticas y a partir de ellas formulan y solucionan problemas” (p.75), de tal manera que se hace un llamado para que se le permita a los estudiantes, partiendo de las soluciones que propongan, justificar, explicar y argumentar. En este sentido, se reconoce una vez más el sentido e importancia que debe asignársele a los procesos que se esconden tras una respuesta, más que a la misma respuesta independientemente de que ésta sea correcta o incorrecta, en correspondencia con Kilpatrick, Gómez & Rico (1998), todo con el ánimo de identificar la naturaleza de posibles dificultades asociadas al aprendizaje de las matemáticas, concretamente en relación a los números enteros, en los casos que aplique.

CONCLUSIONES

Partiendo del recorrido bibliográfico realizado en el presente artículo y la experiencia como docente, concluyo que nos encontramos frente a un desafío educativo en relación a los procesos que se desarrollan en el área de matemáticas, concretamente en lo que tiene que ver con el concepto de números enteros, y no porque sea algo nuevo, sino porque precisamente se requiere tener claridad frente a la naturaleza de dificultades asociadas al aprendizaje de los mismos, en cuanto no es posible generalizar con dificultades de aprendizaje una conducta o manifestación que tal vez no lo sea y, para ello, es necesario disponer de herramientas que favorezcan su identificación.

Si bien desde el Ministerio de Educación, en el caso de Colombia, disponemos de una serie de documentos que orientan la enseñanza de las matemáticas en los niveles de educación básica y media, es importante recordar que existen diversos estilos de aprendizaje, así como de enseñanza, y en ese sentido es posible percibir la multiplicidad de situaciones que pueden presentarse durante el proceso, especialmente en el caso de los estudiantes, dado que en la medida que se logre identificar la razón o naturaleza que se esconde tras las diferentes manifestaciones que recibimos de parte de ellos, bien sea en lo que hacen, lo que dicen, incluso en lo que dejan de hacer y en sus silencios, y en asociación con lo que Claxton (2001) define como recursos tanto internos como externos, los cuales pueden ejercer influencia en su aprendizaje, se favorecerá la atención desde el aula de clase ante esas posibles dificultades, teniendo presentes las regularidades que puedan reconocerse y en base a ellas realizar la posterior categorización.

En el papel de docentes debemos prestar especial atención a dichas manifestaciones, a la forma como evaluamos y verificamos el aprendizaje, teniendo en cuenta que existen diversos factores que pueden influir en los resultados obtenidos y ello dependiendo también del método utilizado. Si bien la prueba escrita es una de las principales herramientas utilizadas para evaluar aprendizajes, utilizada incluso por diferentes estamentos del gobierno, por ejemplo, con las Pruebas SABER y exámenes de ingreso a la carrera oficial, a parte de medir conocimientos importan los procesos que se esconden tras una respuesta y de allí la necesidad de variar también los métodos, en los que la observación y la verbalización pueden ser de utilidad, contrastar una respuesta y permitirle al estudiante que comunique, si es el caso, aspectos que pueden ser tenidos en cuenta para identificar la causa o naturaleza de una posible dificultad.

REFERENCIAS BIBLIOGRÁFICAS

• Blakemore, S. J. (2008). Cómo aprende el cerebro. Las claves para la educación. Barcelona: Ariel.

• Claxton, G. (2001). Aprender. El reto del aprendizaje continuo. España: Editorial Paidós.

• Dehaene, S. (2016). El cerebro matemático: Cómo nacen, viven y a veces mueren los números en nuestra mente. Argentina: Siglo Veintiuno Editores.

• Duval, R. (2016). Un análisis cognitivo de problemas de comprensión en el aprendizaje de las matemáticas.

• Fernández Carreira, C. (2003). Principales dificultades en el aprendizaje de las Matemáticas. Pautas para maestros de Educación Primaria. Barcelona.

• Fonseca Tamayo, F. L. (2019). La discalculia un trastorno específico del aprendizaje de la matemática. ROCA, 212-224.

• Hudson, D. (2017). Dificultades específicas de aprendizaje y otros trastornos. Madrid: Narcea.

• Hudson, D. (2017). Dificultades específicas de aprendizaje y otros trastornos. Madrid: Narcea.

• Inestroza-Inestroza, F. A. (2018). Creencias pedagógicas respecto de las dificultades específicas del aprendizaje de las matemáticas desde la perspectiva de las educadoras diferenciales en una escuela pública de Chile. Revista Electrónica Educare, 265-286.

• Kilpatrick, J. G. (1998). EDUCACIÓN MATEMÁTICA Errores y dificultades de los estudiantes Resolución de problemas Evaluación Historia. Bogotá: Grupo Editorial Iberoamérica.

• Minayo, M. C. (2010). Los conceptos estructurantes de la investigación cualitativa. Salud colectiva, 251-261.

• Nacional, M. d. (1998). Lineamientos curriculares Matemáticas. Bogotá: MEN.

• Nacional, M. d. (2006). Estándares Básicos de Competencias en Matemáticas. Bogotá: MEN.

• Ortiz, L., Ramírez, M., Joya, A., Celi, V., Acosta, M., Perdomo, A., & Morales, D. &. (2013). Los Caminos del Saber Matemáticas 7. Bogotá: Santillana S. A.

• Palencia M, G. E. (2019). Estudio sobre referentes conceptuales en prácticas evaluativas que posicionan a estudiantes con dificultades de aprendizaje en matemática.

• Romero Pérez, J. F. (2004). Dificultades en el aprendizaje: Unificación de Criterios Diagnósticos. España: Junta de Andalucía.

• Romero Pérez, J. F. (2004). Dificultades en el Aprendizaje: Unificación de Criterios Diagnósticos. España: Junta de Andalucía.

• Sampieri, R. F. (2010). Metodología de la Investigación (5ta. ed.). México D. F.: Mc Graw Hill.

• Schunk, D. H. (2012). Teorías del aprendizaje Una perspectiva educativa. México: Pearson.

• Schunk, D. H. (2012). Teorías del aprendizaje. Una perspectiva educativa. México: Pearson Educación.

• Sepúlveda, A. O.-L. (2016). ¿A qué atribuyen los estudiantes de educación básica la dificultad de aprender matemática? Revista de Orientación Educacional, 105-119.

• Strauss, A. y. (2016). Bases de la investigación cualitativa: técnicas y procedimientos para desarrollar la teoría fundamentada. Colombia: Universidad de Antioquia.

ORATORES ISSN Impreso: 2410-8928 ISSN Electrónico: L-2644-3988 Año 9. Número 14. Junio - Noviembre 2021