MEDIACIÓN DIDÁCTICA
DE LA HERRAMIENTA GEOGEBRA
EN EL CONCEPTO DE PERÍMETRO: ESTUDIO DE CASO
|

|
Sonia Ayadide Ríos Forero
Institución Educativa Departamental José María Obando El Rosal Cundinamarca
riosforero12@gmail.com
ORCID: 0000-0001-7386-3032
|
|
|
|
|

|
David
Alberto García Arango
Corporación Universitaria Americana
dagascorpion@gmail.com
ORCID:0000-0002-0031-4275
|
DOI: 10.37594/oratores.n15.501
Fecha de recepción:02/07/2021 Fecha de revisión:05/08/2021 Fecha de aceptación:24/09/2021
RESUMEN
La presente investigación surge a
partir de los bajos resultados de pruebas saber 2017, en el área de matemáticas en los grados
3° y 5 así como la identificación de escasa utilización de recursos didácticos basados en TIC. La
investigación tuvo como objetivo analizar el nivel de mediación didáctica de la herramienta GeoGebra en la conceptualización de perímetro en los
estudiantes de grado quinto de una
Institución Educativa de Colombia. A
nivel metodológico, se consideró un enfoque de investigación mixto con diseño experimental donde se partió de la conformación de dos grupos: un grupo experimental y uno de control con dos fases:
una longitudinal tomando
datos antes y después de la intervención de la
mediación; otra transversal en el sentido en que son analizados al unísono dos grupos denominados grupo
control y grupo experimental. Como instrumentos o materiales de investigación, se tomó una primera medición o pretest basada en cuestionarios de evaluación diagnóstica de geometría y un cuestionario de
evaluación motivacional del proceso de aprendizaje. Posteriormente se trabajó con el grupo
experimental utilizando las TIC, específicamente considerando el uso de la herramienta GeoGebra. Con el grupo de control
se adelanta el desarrollo de las temáticas
de forma convencional (lápiz, cuaderno, regla) aplicando la misma guía de trabajo.
Se abordó la conceptualización de perímetro en condiciones similares y
utilizando la plataforma Google Meet, aplicando finalmente una prueba postest;
con esta información se realizó el análisis
de las variaciones en el nivel de comprensión del concepto de perímetro.
Como resultado, se identificaron niveles
de avance significativos del grupo experimental en comparación con los datos obtenidos para estudiantes del
grupo control. La investigación concluye un nivel significativo de avance en los estudiantes del grupo
experimental, verificando de esta forma la importancia de la mediación
de la herramienta GeoGebra en la enseñanza del concepto.
Palabras Clave: GeoGebra; aprendizaje; perímetro; pensamiento geométrico; mediación didáctica
DIDACTIC MEDIATION OF GEOGEBRA SOFTWARE IN THE
CONCEPT OF PERIMETER: CASE STUDY
ABSTRACT
This research arises from the low results of saber 2017 tests, in the area of mathematics in grades 3 and 5, as well
as the identification of low use of ICT-based teaching resources. The objective of the research was to analyze the level
of didactic mediation of GeoGebra tool in the conceptualization of perimeter in
fifth-grade students of an Educational Institution in Colombia.
At a methodological level, a mixed research approach with an experimental design was
considered
where it was started from
the conformation of two groups: an
experimental group and a control group with two phases: a longitudinal one, taking data before and after the mediation intervention; another cross-sectional in this matter, two groups called control group and experimental group are both analyzed. As instruments or research materials, a first measurement or pre-test was taken based on questionnaires
for the diagnostic
evaluation of geometry and
a questionnaire for motivational evaluation of the learning process. Later, this questionnaire has been taken in account the experimental group using ICT, specifically considering the use of the GeoGebra tool. With the control group, the development of the themes is
carried out in a conventional way (pencil, notebook,
ruler) applying the same work
guide. The perimeter conceptualization was approached using similar conditions and with Google Meet platform, finally applying a post-test; With this information, the
analysis of the variations in the level of understanding of the concept of perimeter was carried out.
As a result, significant levels of advancement of the experimental group were identified in comparison with the data obtained
for students of the control group. The research concludes a significant level of progress in the students of the experimental group, thus verifying the importance of the mediation of the GeoGebra tool in teaching the concept.
Keywords: GeoGebra; learning; perimeter; geometric thinking; didactic mediation
INTRODUCCIÓN
Inicialmente vale la pena realizar un recorrido histórico
de la mediación de las tecnologías digitales
en la educación colombiana, haciendo mención a los grandes cambios que
han permitido la transformación de las prácticas educativas, es así que se parte
de la lectura, utilizando el papel y el
lápiz, pasando al avance de la radio y la televisión, medios que hicieron
posible el paso de una educación presencial a la no presencial, posteriormente con la utilización de medios audiovisuales como: la televisión, radio, cine, proyectores de películas y diapositivas, da origen a las Tecnologías Educativas, luego
aparece el internet,
se integró el uso de computadores en las instituciones, se dio la comunicación textual, presentaciones en Power Point y uso de medios digitales, pero manteniéndose aún una educación oral tradicionalista,
para posteriormente llegar a las TIC como herramienta de enseñanza en el uso de redes sociales, buscadores web y las denominadas plataformas virtuales que se
utilizan en la actualidad y que con la masificación del Internet da paso a la
aparición de nuevas herramientas
digitales para la colaboración y la co-creación de
entornos virtuales de aprendizaje.
En el marco de lo anterior y
considerando la importancia del uso de herramientas digitales para el aprendizaje y de acuerdo
con los resultados en las pruebas
saber 2017, en el grado
3° y 5°, donde se pudo
evidenciar que en la Institución Educativa José María Obando existe bajo rendimiento académico en el área de matemáticas, en especial en el pensamiento geométrico. La
presente investigación tiene como objetivo principal aportar al análisis y
comprensión de los niveles de
apropiación de la herramienta GeoGebra como mediadora
en el fortalecimiento del pensamiento geométrico en estudiantes de grado quinto.
Apoyados en los objetivos específicos de identificar variables que intervienen en los procesos de
mediación didáctica para el desarrollo del
concepto de perímetro en el área de matemáticas, analizar la incidencia de la
mediación de la herramienta GeoGebra en las variables
que intervienen en la conceptualización de perímetro en los estudiantes, analizar la incidencia de la
mediación de herramientas de enseñanza convencionales en las variables
que intervienen en la conceptualización de perímetro en los estudiantes y comparar los niveles de mediación de las
herramientas analizadas para la conceptualización de perímetro en los estudiantes.
Desde esta perspectiva, es posible considerar el mejoramiento del rendimiento académico, los resultados en las pruebas
aplicadas en matemáticas, potenciar el proceso
de enseñanza aprendizaje, despertar el interés y promover un mejoramiento en la
percepción de los estudiantes hacia las matemáticas, facilitando el aprendizaje mediante
representaciones virtuales que permitan un acercamiento a la aplicación de los conceptos en situaciones reales.
Para finalizar es importante recalcar
que la presente investigación surge como respuesta a la necesidad de reconocer el rol preponderante de las
herramientas basadas en Tecnologías Digitales
en los procesos de mediación para la enseñanza de conceptos geométricos.
REVISIÓN
DE LA LITERATURA
Al referirnos a la palabra didáctica la
relacionamos con contenidos didácticos, material y juegos didácticos. Es un término
que es fundamental en el proceso de enseñanza-aprendizaje y para el docente es esencial en su práctica
pedagógica porque debe crear las estrategias de aprendizaje más
adecuadas para que los estudiantes aprendan a aprender, construyan aprendizajes
significativos, dentro un
clima agradable, a partir de su contexto y con el uso de estrategias para el
desarrollo de competencias. En este
contexto, el término didáctica contribuye a “enriquecer
el saber sobre la tarea concreta a desarrollar en el
aula de clase” (Celi,
2012, pág. 63)
Por
lo anterior, se considera que, la mediación didáctica constituye el proceso de enseñanza- aprendizaje que se establece siempre en
ámbitos de relación entendidos como nexo global, como circunstancia que sirve de unión, como conexión o contacto entre
los elementos personales que configuran
ese proceso (profesor/alumno) y herramienta educativa, entre estos y el resto
de los elementos de dicho proceso:
contenidos, actividades, recursos y evaluación. (Soto, 1999)
Para este trabajo, el recurso didáctico
utilizado para llevar a cabo la temática
en geometría se da por medio
de la herramienta didáctica GeoGebra.
La mediación didáctica es tender
puentes de relación e interacción entre lo que el estudiante conoce y no conoce, entre lo vivido y lo
que va a vivir , para lo cual se deben trabajar en crear actividades de aprendizaje donde el docente
dé explicaciones claras
y precisas sobre
lo que se desee realizar
, permitir un diálogo, adecuar
los espacios y las situaciones que participan en el aprendizaje y plantearse interrogantes como: ¿con quién se aprende?, ¿con
qué se aprende?, ¿en qué momento se aprende?, para facilitar el camino en la
aplicación de la mediación didáctica (Roca, 2012). la mediación o utilización de la herramienta GeoGebra; se inician mencionando el creador de esta herramienta, quien la presentó
para un trabajo de tesis, como fuente de apoyo a la didáctica de las matemáticas, el software ha sido ganador
de varios premios,
desatacando su versatilidad de aplicación y uso en niveles de primaria hasta universidad. Seguidamente, se presentan investigaciones a nivel internacional, nacional y local. En los artículos y trabajos identificados, se llevan a cabo diseños de investigación con grupos control y
experimental del uso aplicación en entornos áulicos,
dando a conocer
los hallazgos en el marco
del mejoramiento de los aprendizajes, así como el fortalecimiento de competencias y pensamientos a
través de variadas experiencias. Igualmente
se determinan e identifican los avances, hallazgos, aportes, conclusiones y
nuevos desafíos relacionados con las TIC y la herramienta GeoGebra.
Es así como, se sigue los postulados de John
Dewey, quien establece que la educación está
basada en la experiencia real y afirma que, si hay alguna duda, respecto
a cómo el aprendizaje sucede, hay que
involucrarse, estudiar, ponderar, considerar posibilidades alternas y llegar a
sus posiciones basados en evidencia sólida; es así que, cuestionarse es la clave en el aprendizaje activo.
Ahora bien, al integrar el concepto
de TIC en este enfoque de la pedagogía activa, las Tecnologías de la Información y la Comunicación adquieren un
significado importante, haciendo un papel de mediación
didáctica, ya que promueven y facilitan el aprendizaje y motiva al estudiante para que sea actor de su proceso
de aprendizaje. Éstas
se convierten en un medio
para compartir sus saberes
trabajar no solo de forma individual sino colaborativa. Además,
al hacer uso de herramientas informáticas como lo es GeoGebra, se
convierten en mediadores del aprendizaje, específicamente en el campo de la geometría,
permitiéndole que vivencie sus saberes en espacios virtuales, pero a su vez
sean simuladores de contextos
cotidianos y vivenciales.
Para Vygotsky, existe relación entre
el objeto de conocimiento y el sujeto. También se encuentra al respecto el planteamiento interaccionista
dialéctico objeto sujeto (O—S), en la cual hay
una relación de recíproca influencia, a dicha relación autores como Yaroshevsky (Hernandez, 1997), denominada la actividad objetual.
De esta manera, los procesos de
enseñanza y aprendizaje establecen una relación entre el sujeto y el objeto de conocimiento. Esta relación está mediada por la actividad que el sujeto
realiza sobre el objeto de conocimiento, para ello se vale de diferentes instrumentos socioculturales. Dicho instrumento, Vygotsky las denomina
herramientas y signos (ver figura 3), la primera (herramienta) orienta la actividad
del sujeto y la segunda
(el signo) genera cambios en el sujeto que efectúa
dicha actividad al interior de este según (Hernandez,
1997).
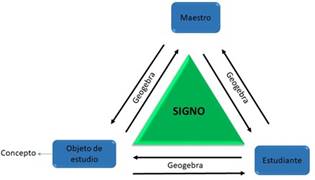
Figura 1. Esquema relacional entre estudiante, objeto
de estudio y maestro en el marco
de la mediación basada en
GeoGebra. Elaboración
propia
Según la figura 1, el Esquema relacional entre
estudiante, objeto de estudio y maestro en el
marco de la mediación basada en GeoGebra, en el proceso de enseñanza
está planteado a partir del objeto de estudio: la conceptualización de perímetro, pasa a través
de los ojos del maestro
por medio de GeoGebra, dándole una
transformación e interpretación a este conocimiento o aprendizaje para que a través de la mediación de GeoGebra llegue al estudiante y este acceda al conocimiento; es un ciclo o actividad que
permite la retroalimentación continua. En el proceso de aprendizaje, el estudiante es el que empieza a interactuar con el objeto de estudio:
conceptualización de
perímetro con la mediación de la herramienta GeoGebra,
realimenta su proceso a través del dialogo,
explicación, orientación dada por el docente, y éste a su vez retoma esos
conocimientos que el estudiante
genera a partir del trabajo con GeoGebra, para luego
resignificar el objeto de estudio y
hacer una nueva elaboración de los conceptos, teniendo en cuenta que al inicio
el objeto de estudio el estudiante
no lo reconoce, con la aplicación y mediación de GeoGebra
se apropia gradualmente del
conocimiento. El triángulo es equilátero para representar un equilibrio entre
los participantes del proceso. El
signo que representa el concepto de perímetro en sus inicios o nivel real del aprendizaje es mínimo, a medida que se da el proceso
de aprendizaje y se va avanzando de forma ágil, aumenta el nivel de apropiación
del concepto y se proyectará a nuevos saberes.
Este
esquema también se plantea para la conceptualización de perímetro a través de la forma convencional
utilizando como mediación: compás, regla, tablero, cuaderno, lápiz entre otros,
de forma equilibrada y llevado
al proceso de enseñanza – aprendizaje. Parte del objetivo
del desarrollo del trabajo es contrastar los resultados
obtenidos de estas relaciones en entornos mediados por GeoGebra en contraposición con entornos mediados,
métodos y técnicas
convencionales de enseñanza.
Es así como, la mediación dada en los
procesos de aprendizaje se ve reflejada en acciones como, la comunicación entre estudiante y el mediador; esta
intervención debe impulsar a la participación,
la creatividad, la justificación o explicación, a través del diálogo y una
interacción entre el estudiante y el conocimiento. Gadamer (Fainholc, 2004) destaca que el trabajo
interpretativo brinda
elementos sobre el “dialogo” en la
medida en que el individuo a partir de la interpretación establece un vínculo a través de preguntas y respuestas que
conllevarán un mejor entendimiento.
De
esta manera, Vygotsky
aclara que en todo proceso
educativo participan tres componentes primordiales como agentes mediadores: el agente que aprende (el estudiante), el agente que enseña (el docente) y lo que se aprende
o se enseña (los contenidos curriculares). (Chaves Salas,
2001). En este artículo
se presentará el rol de Geogebra en el marco de la mediación.
METODOLOGÍA
El diseño de la investigación es de campo,
longitudinal en el sentido en que se realizaron análisis
antes y después de una intervención de mediación basada en Geogebra y transversal en el sentido en que fueron analizados al unísono dos grupos: grupo control y
grupo experimental. Respecto al enfoque
es de tipo mixto. Con el grupo control se trabajó utilizando estrategias
convencionales o tradicionales en la enseñanza del concepto de perímetro, con el grupo
experimental se adelantó
un trabajo apoyado en la herramienta GeoGebra.
En este sentido,
el diseño de la investigación corresponde, según la clasificación de Campbell y Stanley (Gage, 1967) a un diseño experimental verdadero con grupo control con pretest y postest. En este diseño, la muestra es elegida a
conveniencia en el sentido en que se controla la variable docente interviniendo únicamente los
grupos en los cuales el docente investigador imparte la asignatura, seleccionando dos grupos similares en desempeño académico, de esa manera,
se evita la inclusión de la variable
docente. La relación
temporal en la medición de las variables
es simultánea y según el número de variables a
considerar, el diseño es multivariado. La Tabla 1 representa las características del diseño de investigación. El símbolo “O” representa la generación de observación o medida
y el símbolo “X” representa
tratamiento.
Tabla 1. Diagrama del diseño
experimental. Elaboración propia
|
Grupo
|
Momento I
|
Momento II
|
Momento III
|
|
Experimental
|
O
|
X
|
O
|
|
Control
|
O
|
|
O
|
Puede observarse entonces que en el Momento
II, se genera tratamiento al grupo experimental aplicando la herramienta Geogebra. Al indicar tratamiento es importante aclarar
que si bien es cierto
a ambos grupos se les explica la temática, solo uno de ellos trabaja con
Geogebra. En la Figura 2, se describe el proceso de investigación, incluyendo los aspectos de validación de los instrumentos.
La implementación del diseño del
estudio intervino 73 estudiantes, de los grados quintos jornada tarde, 501 JT 36 estudiantes, 27 hombres y 9 mujeres
– 502 JT, 37 estudiantes 22 hombres y 15 mujeres, con edades que oscilan
entre 10 y 14 años.
Los estudiantes participantes de las pruebas están registrados de la siguiente manera: Prueba diagnóstica de geometría: 44 participantes, 501 JT experimental: 23 estudiantes y 502
JT control: 21 estudiantes.
Cuestionario de evaluación motivacional del proceso de aprendizaje (EMPA)
pretest: 44 participantes.
Prueba final de geometría: 36 participantes. 501 JT experimental: 19 estudiantes y 502 JT
control:
17 estudiantes.
Prueba final motivacional: 22 participantes de 501 JT
A continuación,
se presentarán los resultados obtenidos del
desarrollo de la investigación en el
marco del concepto de mediación didáctica.
RESULTADOS
Aplicando el diseño de experimentos propuesto en
la metodología, se tienen dos escenarios en
los cuales para cada muestra por separado se aplicó un análisis de prueba T
para muestras relacionadas. Con este análisis
se pretende identificar si el promedio
de los resultados de la prueba diagnóstica es significativamente diferente a los resultados de la prueba
final. Para tener resultados estandarizados en cada una de las pruebas, se procedió a dividir la cantidad de preguntas acertadas por cada estudiante entre la cantidad
total de preguntas
de la prueba para el caso de la prueba
sin validación y para el caso de pruebas validadas se dividió la
cantidad de preguntas acertadas por
cada estudiante entre la cantidad total de preguntas validadas por los
expertos. Vale la pena recordar que,
para el caso de la prueba diagnóstica, el número de preguntas validadas fue 5 y
para el caso de la prueba
final, el número de preguntas validadas fue 6.
Antes de ese análisis
se verifican los siguientes resultados en promedios:
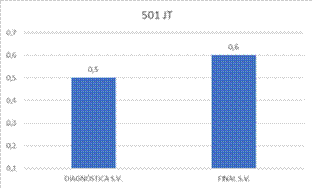
Figura 3. Promedio de prueba
diagnóstica y final
sin validación para el grupo experimental.
Elaboración propia.
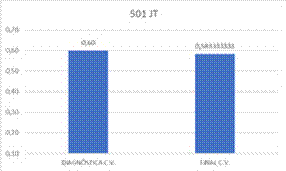
Figura 4. Promedio de prueba
diagnóstica y final
con validación para el grupo experimental
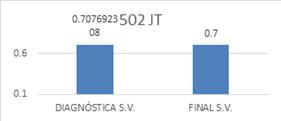
Figura 5. Promedio de prueba
diagnóstica y final sin validación para el grupo control.
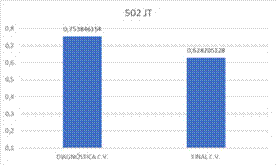
Figura 6. Promedio de prueba diagnóstica y final con validación para el grupo control
Con base en las gráficas anteriores, es posible
identificar que si bien es cierto, los resultados son mejores a nivel comparativo para 502 que para 501, se observa
un nivel significativo de avance en los estudiantes del grupo experimental
(501), este avance se verifica en el sentido en que los resultados obtenidos por el grupo
experimental se mantuvieron estadísticamente similares en las pruebas
validadas, tanto en la prueba diagnóstica (0,60) como en la prueba final (0,58) bajo el entendido que la prueba final es
significativamente más compleja que la prueba diagnóstica. Igualmente, se puede ver cómo el promedio para las pruebas
sin validación incrementa (pasa de 0,5 a
0,6). Si se hace el mismo análisis para 502, se observan resultados
estadísticamente similares en la prueba
sin validación y se observa
un decrecimiento en los resultados comparativos de la prueba diagnóstica (0,75) con la prueba final (0,62) teniendo
en cuenta las preguntas con validación. Es importante recordar que las pruebas con
validación corresponden a las preguntas que según los expertos evalúan mejor
el concepto de perímetro dándole
más peso al decrecimiento observado
en el grupo 502.
Para complementar mejor las
relaciones anteriormente expresadas, se hace la siguiente prueba de hipótesis
utilizando la prueba
T para muestras relacionadas con un 90% de significancia estadística, en este sentido, (Kraska-Miller, 2013,
pág. 111) Propone que:
El investigador fija los límites del
intervalo de confianza. El que se usa más frecuentemente en ciencias sociales
y del comportamiento es del 95%; sin embargo, un 90% y 99% de intervalos de confianza también son utilizados basándose en el
criterio del investigador quien decide el porcentaje deseado según las condiciones del problema que se está
analizando. En el caso específico de la presente
investigación, se ha definido como intervalo de confianza un 90% debido al
limitado tamaño de la muestra
y las condiciones de recolección de datos debidas
a la conectividad de trabajo
en casa en el marco
de la crisis sanitaria por COVID-19. A continuación, se presentan los resultados de la aplicación del software SPSS para
la comparación de medias con prueba T para muestras relacionadas con sus respectivas hipótesis.
Para el grupo experimental:
H0: Los promedios
de la prueba diagnóstica y la prueba
final son iguales
para 501 JT H1:
Los promedios de la prueba diagnóstica y la prueba final son diferentes 501 JT Los resultados
obtenidos se presentan en la Tabla 2.
Tabla 2. Resultados de prueba
T para el grupo experimental.
|
Prueba de muestras emparejadas
|
|
|
Diferencias emparejadas
|
t
|
gl.
|
Sig.
(bilateral)
|
|
Media
|
Desv.
|
Desv. Error
promedio
|
90% de intervalo de confianza de la diferencia
|
|
Inferior
|
Superior
|
|
Par 1
|
Puntuación Diagnóstica sin validación estandarizada -
Puntuación Final
sin validación
estandarizada
|
-0,100
|
0,249
|
0,0589
|
-,0,2024
|
0,0024
|
-1,699
|
17
|
0,108
|
|
Par 2
|
Puntuación Diagnóstica con validación estandarizada -
Puntuación Final
con validación
estandarizada
|
0,025
|
0,340
|
0,08032
|
-0,16566
|
0,11381
|
-0,323
|
17
|
0,751
|
Según los resultados de la Tabla 2, tanto para la
prueba sin validación como para la prueba con
validación, se obtiene un p-valor superior a 0,1 en el cual los respectivos
intervalos para cada par de pruebas
son a saber: para la prueba sin validación (-0,2024; 0,0024) y para la prueba
con validación (-0,16566; 0,11381). En ese sentido
se observa que los intervalos contienen el cero con lo cual se acepta la hipótesis nula “Los
promedios de la prueba diagnóstica y la prueba final son iguales para 501 JT”.
Para el grupo control:
H0: Los promedios de la prueba diagnóstica y la prueba
final son iguales para 502 JT H1: Los promedios de la prueba
diagnóstica y la prueba final son diferentes para 502 JT
Tabla 3. Resultados de prueba
T para el grupo control
|
Prueba de muestras emparejadas
|
|
|
Diferencias emparejadas
|
t
|
gl.
|
Sig.
(bilateral)
|
|
Media
|
Desv.
|
Desv. Error
promedio
|
90% de intervalo de confianza de la diferencia
|
|
Inferior
|
Superior
|
|
Par 1
|
Puntuación Diagnóstica sin validación estandarizada -
Puntuación Final
sin validación
estandarizada
|
0,007
|
0,18
|
0,0512
|
-0,0836
|
0,0990
|
0,150
|
12
|
0,883
|
|
Par 2
|
Puntuación Diagnóstica con validación estandarizada -
Puntuación Final
con validación
estandarizada
|
0,125
|
0,24
|
0,0675
|
0,00527
|
0,246002
|
1,860
|
12
|
0,087
|
Según los resultados de la Tabla 3, para la prueba sin validación se obtiene un p-valor superior
a 0,1 con lo cual se acepta la hipótesis nula “Los promedios de la
prueba diagnóstica y la prueba final
son iguales para 502 JT”; sin embargo, para la prueba con validación, se
obtiene un p-valor inferior a 0,1 e
igual a 0,087 con lo cual se rechaza la hipótesis nula indicando que para la
prueba con validación “los promedios
de la prueba diagnóstica y la prueba final son diferentes para 502 JT”. Las aseveraciones anteriores se verifican
teniendo en cuenta
los siguientes intervalos:
Sin validación: (-0,836; 0,0990)
Con
validación: (0,0527; 0,246002)
Los valores anteriores muestran cómo el cero está
en el intervalo sin validación pero no está
en el intervalo con validación, lo cual apoya
el hecho de considerar que el puntaje
de la prueba con validación desmejoró significativamente al compararse en su etapa diagnóstica y su etapa final para
502JT, lo cual si es interpretado en términos del nivel de dificultad de las pruebas
y se compara con el comportamiento de los resultados de
éstas para 501JT, observamos que éste último se mantuvo estable en puntaje lo cual demuestra un mejoramiento en el
desempeño del grupo.
CONCLUSIONES
Al analizar el nivel de mediación didáctica de la herramienta Geogebra en la conceptualización de perímetro en los estudiantes de grado quinto
de la IED José María
Obando El Rosal
Cundinamarca, se obtuvo
un mejor desempeño en cuanto al nivel de avance del mismo grupo 501 JT, con respecto
al grupo de control 502 JT, es de mencionar que la muestra es muy
pequeña teniendo en cuenta los participantes de cada grado para el registro de las pruebas
para lo cual se realizaron las debidas acciones y análisis estadísticos que
permitieron una mejor validación de los resultados.
En
la identificación de variables que intervienen en los procesos
de mediación didáctica
para el desarrollo del
concepto de perímetro en el área de matemáticas, se trabajó a nivel
cuantitativo con la variable de
desempeño académico, a través de la prueba diagnóstica pretest
y la prueba final postest
de geometría, aplicando la herramienta Geogebra como
mediadora en 501 JT y la enseñanza
convencional en 502JT. A nivel cualitativo se implementó el cuestionario de evaluación motivacional del proceso de aprendizaje, instrumentos que analizados en sus resultados permitieron dar el
análisis correspondiente.
En
el análisis de la incidencia de la mediación
de herramientas de enseñanza convencionales en las variables que intervienen en la conceptualización de
perímetro en los estudiantes de grado quinto de IED José María Obando
El Rosal Cundinamarca, se obtuvo que el grado 502JT de control,
en la prueba sin validación obtuvo resultados estadísticamente similares
observándose además un decrecimiento en la prueba con validación, en los resultados comparativos de la prueba diagnóstica con la prueba final, de esta forma se obtiene para 502 el intervalo con validación (0,0527;
0,246002) en el cual se observa una diferencia significativa de promedio con respecto al grupo experimental.
REFERENCIAS BIBLIOGRÁFICAS
•
Celi, A. (2012). Fundamentos de pedagogía y didáctica. Guía didáctica. Loja Ecuador:
EDILOJA Cía Ltda.
Obtenido de http://www.ediloja.com.ec
•
Chaves Salas, A. (2
de Septiembre de 2001). Implicaciones educativas de la teoría sociocultural de Vigotsky. Revista
Educación(25), 59-65. Obtenido
de redalyc.org/ pdf/440/44025206.pdf
•
Fainholc, B. (2004). Lectura crítica en Internet. Análisis y utilización
de los recursos tecnológicos en educación. Argentina: Homo sapiens.
•
Gage, N. L. (1967).
Handbook of Research on Teaching. Chicago:
Rand McNally.
•
Hernández, G. (1997).
Módulo Fundamentos del Desarrollo de la Tecnología Educativa (Bases Psicopedagógicas). Mexico: Ediciones ILCE- OEA. Obtenido de https://www. monografias.com/docs/Ern%C3%A1ndez-rojas-gerardo-m%C3%B3dulo-fundamentos- del-desarrollo-P3MP6U7VPNAX
•
Kraska-Miller, M. (2013). Nonparametric statistics for social and behavioral sciences. New York: Taylor & Francis Group.
•
Roca, R. M. (2012).
El problema de enseñar y aprender ciencias
naturales en los nuevos ambientes educativos. Argentina: Universidad Nacional de la Plata. Obtenido
de http://sedici.unlp.edu.ar/bitstream/handle/10915/18190/Documento_completo. pdf?sequence=3
•
Soto, G. (1999). Más allá del currículo: La educación ante el reto de las nuevas tecnologías de la información y la comunicación. Caracas: Pirámide Poblacional de Venezuela.
ORATORES ISSN Impreso: 2410-8928 ISSN Electrónico: L-2644-3988 Año 9. Número 15. Diciembre 2021- Mayo 2022